安徽省滁州二中高中数学《32立体几何中的向量方法》课件(4)新人教A版选修2-1VIP免费

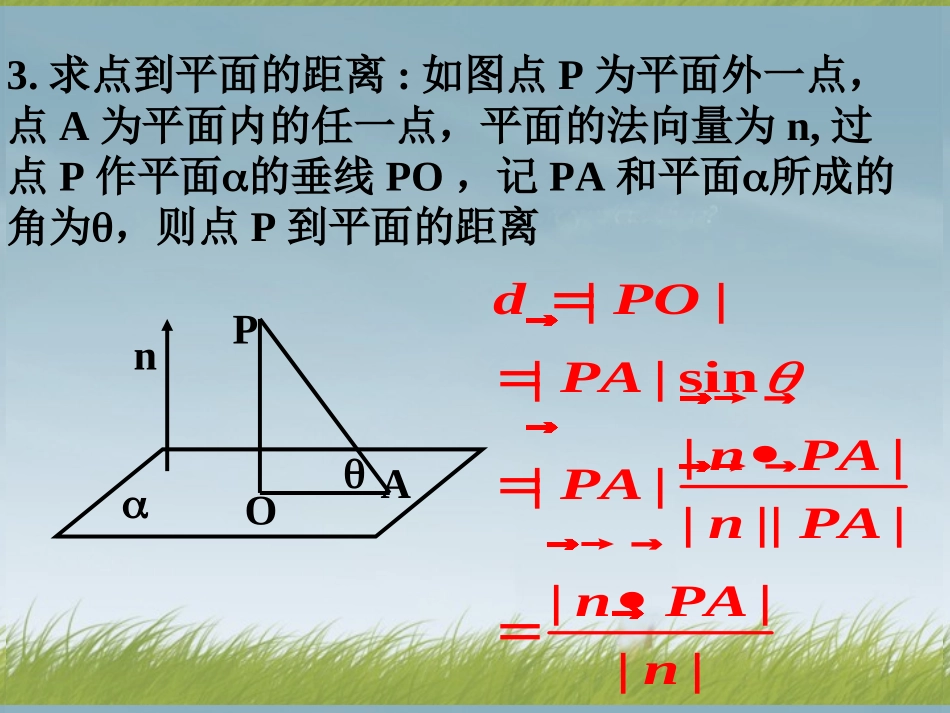
-----利用向量解决空间的距离问题3.2立体几何中的向量方法(四)向量法求空间距离的求解方法1.空间中的距离主要有:两点间的距离、点到直线的距离、点到平面的距离、直线到平面的距离、平行平面的距离、异面直线间的距离.其中直线到平面的距离、平行平面的距离都可以转化点到平面的距离.2.空间中两点间的距离:设A(x1,y1,z1),B(x2,y2,z3),则222121212()()()ABxxyyzz�||||sin||||||||||||dPOPAnPAPAnPAnPAn����������3.求点到平面的距离:如图点P为平面外一点，点A为平面内的任一点，平面的法向量为n,过点P作平面的垂线PO，记PA和平面所成的角为，则点P到平面的距离nAPOBAMNnabcos,ABndABABnn��4.异面直线的距离:①作直线a、b的方向向量a、b，求a、b的法向量n，即此异面直线a、b的公垂线的方向向量；②在直线a、b上各取一点A、B，作向量AB；③求向量AB在n上的射影d，则异面直线a、b间的距离为例1：如图1：一个结晶体的形状为四棱柱，其中，以顶点A为端点的三条棱长都相等，且它们彼此的夹角都是60°，那么以这个顶点为端点的晶体的对角线的长与棱长有什么关系？A1B1C1D1ABCD图1解:如图1,不妨设11ABAAAD，1160BAADAA化为向量问题依据向量的加法法则，11ACABADAA�进行向量运算2211()ACABADAA�2221112()ABADAAABADABAAADAA�1112(cos60cos60cos60)6所以1||6AC�回到图形问题这个晶体的对角线的长是棱长的倍。1AC6BAD典例思考：(1)本题中四棱柱的对角线BD1的长与棱长有什么关系？(2)如果一个四棱柱的各条棱长都相等，并且以某一顶点为端点的各棱间的夹角都等于,那么有这个四棱柱的对角线的长可以确定棱长吗?A1B1C1D1ABCD(3)本题的晶体中相对的两个平面之间的距离是多少?(提示：求两个平行平面的距离，通常归结为求点到平面的距离或两点间的距离）11BDBABCBB�1112060ABCABBBBC其中，思考(1)分析:易知对角线1BD的长与棱长的关系.思考(2)分析:1111DAABAABADxAAADABaAC，，设11ACABADAA�由222211112()ACABADAAABADABAAADAA��22232(3cos)axx即136cosxa∴这个四棱柱的对角线的长可以确定棱长.A1B1C1D1ABCDH分析：面面距离转化为点面距离来求.11HACHAA于点平面点作过解：.1的距离为所求相对两个面之间则HA111AAADABBADADAABA且由.上在ACH22()112cos6033ACABBCAC�1111()cos60cos601.AAACAAABBCAAABAABC�1111cos||||3AAACAACAAAC��36sin1ACA36sin111ACAAAHA∴所求的距离是6.3思考(3)本题的晶体中相对的两个平面之间的距离是多少?如何用向量法求点到平面的距离?ABCD1A1B1C1DExyz(1)求B1到面A1BE的距离；例2如图，在正方体ABCD-A1B1C1D1中，棱长为1，E为D1C1的中点，求下列问题：11112(,,)AEABnxyzABE�解=(-1,,0),=(0,1,-1)设为面的法:向量，则110,0,nAEnAB����10,20,xyyz2,2,yxzx即11(1,2,2)xABEn取＝，得平面的一个法向量11110,1,0,BABEAB�选点到面的斜向量为111123ABnBABEdn�得到面的距离为ABCD1A1B1C1DExyz例2如图，在正方体ABCD-A1B1C1D1中，棱长为1，E为D1C1的中点，求下列问题：(2)求D1C到面A1BE的距离；解:D 1C∥面A1BE∴D1到面A1BE的距离即为D1C到面A1BE的距离仿上法求得111113DAnDABEdn�到面的距离为ABCD1A1B1C1Dxyz例2如图，在正方体ABCD-A1B1C1D1中，棱长为1，E为D1C1的中点，求下列问题：(3)求面A1DB与面D1CB1的距离；解: 面D1CB1∥面A1BD∴D1到面A1BD的距离即为面D1CB1到面A1BD的距离111(1,1,1)(1,0,0)ABDnDA�易得平面的一法向量且111133DAnDABDdn�则到面的距离为例2如图，在正方体ABCD-A1B1C1D1中，棱长为1，E为D1C1的中点，求下列问题：(4)求异面直线D1B与A1E的距离.ABCD1A1B1C1DExyz111(0,0,1),(1,1,0),(1,0,1),(0,,...