5.3正弦函数的性质VIP免费

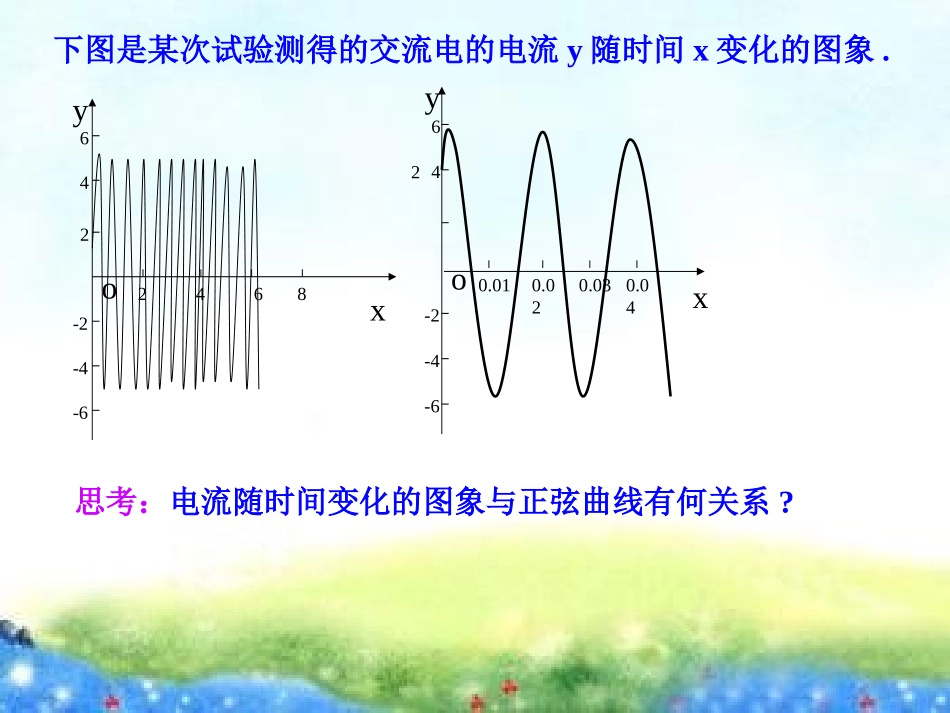
思考：电流随时间变化的图象与正弦曲线有何关系?xo0.010.020.030.04246-6-4-2yxo2468246-6-4-2y下图是某次试验测得的交流电的电流y随时间x变化的图象.正弦型函数：y=Asin(ωx+)正弦型函数y=Asin(ωx+)对于正弦型函数，我们称：为周期2T为频率，21Tf周期T的倒数ωx+为相位，x=0时的相位为初相。角速度，为振幅，ω为A1.y=sin(x+)与y=sinx的图象关系:函数与的图象的变化关系.xysin)6xsin(y),3xsin(y23632y1－1Ox223352613xysin)3sin(xy)6sin(xy所有的点向左(>0)或向右(<0)平移||个单位一、函数y=sin(x+)图象:函数y=sin(x+)(0)的图象可以看作是把y=sinx的图象上所有的点向左(当>0时)或向右(当<0时)平行移动||个单位而得到的.y=sinxy=sin(x+)的变化引起图象位置发生变化(左加右减)平移变换函数、与的图象间的变化关系.xy21sinxysinxy2sin-12yOx241xy21sinxy2sinÕýÏÒÐͺ¯Êý.gspxysin2.y=sinx与y=sinx的图象关系:所有的点横坐标缩短(>1)或伸长(0<<1)倍二、函数y=sinx(>0)图象:函数y=sinx(>0且1)的图象可以看作是把y=sinx的图象上所有点的横坐标缩短(当>1时)或伸长(当0<<1时)到原来的1/倍(纵坐标不变)而得到的.周期变换y=sinxy=sinx纵坐标不变2T决定函数的周期:1/函数、与的图象间的变化关系.xysin21xysinxysin2xO1-1y2-22232xysin2xysin21xysin3.y=Asinx与y=sinx的图象关系:振幅变换y=sinxy=Asinx所有的点纵坐标伸长(A>1)或缩短(00)图象:函数y=Asinx(A>0且A1)的图象可以看作是把y=sinx的图象上所有点的纵坐标伸长(当A>1时)或缩短(当01(伸长0<<1)到原来的1/倍y=sin(x+)纵坐标伸长A>1(缩短00(向右<0)方法:(按顺序变换)Aω,,平移||个单位纵坐标不变横坐标不变1-12-2ox3-36536335612767322y方法2:(按顺序变换)3sin(2)3yxxy2sin62sinπxy62sin3πxyxysinA,,y=sinxy=sin(x+//)横坐标缩短>1(伸长0<<1)到原来的1/倍y=sinx纵坐标伸长A>1(缩短00(向右<0)方法2:(按顺序变换)A,,ω平移个单位纵坐标不变横坐标不变||//1,sin()sin2yxyx函数与的图象有什么关系?13,sinsin3yxyx函数与的图象有什么关系?2,sin3sinyxyx函数与的图象有什么关系?123课堂练习1：如何由变换得的图象？xsiny6x3sin21y课堂练习2：课堂小结:y=sinx所有的点向左(>0)或向右(<0)平移||个单位y=sin(x+)y=sinx所有的点横坐标缩短(>1)或伸长(0<<1)1/倍纵坐标不变y=sinxy=sinx所有的点纵坐标伸长(A>1)或缩短(0