3.3.1正弦函数、余弦函数的图象与性质VIP免费

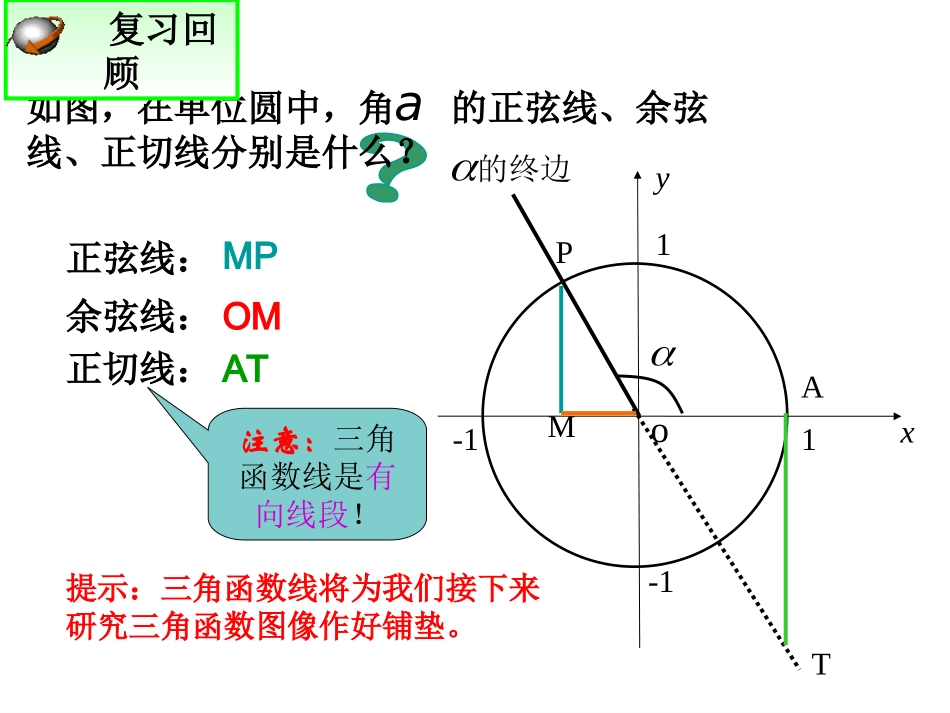
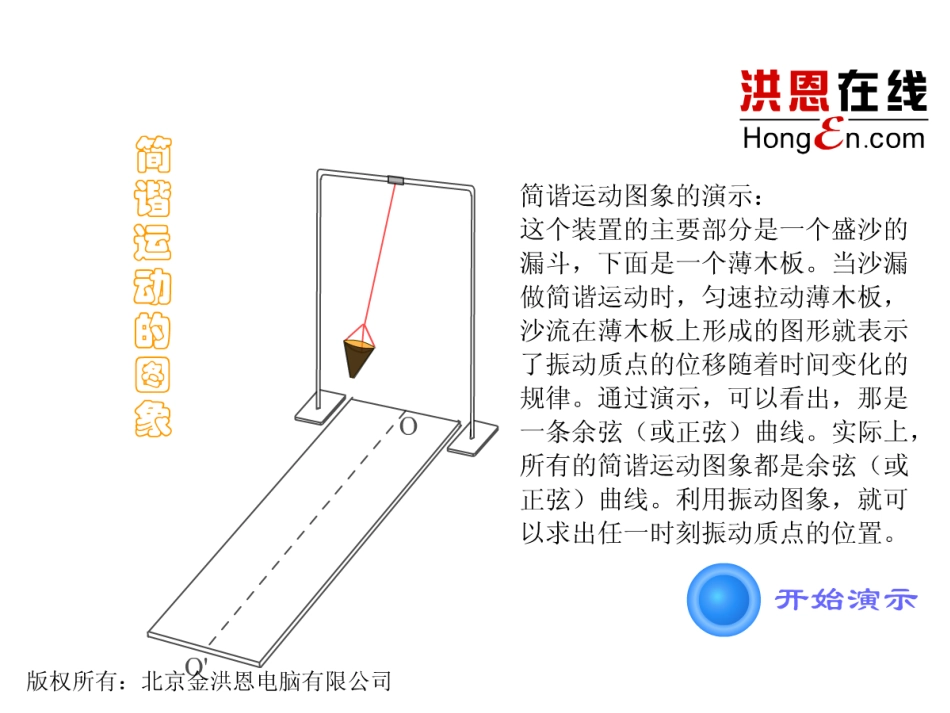
玉林实验中学玉林实验中学叶方华叶方华§1.4.1正弦函数、余弦函数的图象2025年1月21日TMy1xoPA的终边-11-1正弦线：MP余弦线：OM正切线：AT提示：三角函数线将为我们接下来研究三角函数图像作好铺垫。如图，在单位圆中，角的正弦线、余弦线、正切线分别是什么？a复习回顾注意：三角函数线是有向线段！画出y=sinx，x[0,2]的图象新课探究小组小组合作：合作：1.1.合理分工：发言人，记录员，声控员等；合理分工：发言人，记录员，声控员等；2.2.选择选择1~21~2种方法在大卡上作图；种方法在大卡上作图；3.3.每种方法派代表汇报每种方法派代表汇报,,其他补充其他补充,,全班分全班分享享..1-1022322656723352yx●●●一、正弦函数图象y=sinx(x[0,])2332346116633265●●●●●●●673435611●●●1P1M2P2M1.几何法：平移正弦线画y=sinx，x[0,2]图象2、把x轴上0—2π的线段12等份，得到12个点的横坐标.1、把单位圆12等分，并放置于直角坐标系中y轴的左侧.3、把单位圆周上12个点所对的角x的正弦线MP向右平移，使M点与X轴上的点x重合，即可得到12个点.几何画板演示几何画板演示在精确度要求不太高时，选择五点作图法可快捷地作出正弦函数的图象，在作正弦函数的图象时，应抓住哪五个关键点？2.五点作图法与x轴的交点)0,0()0,()0,2(图象的最高点(,1)2图象的最低点3(1)2，sin[0,2]yxx简图作法步骤：(3)连线(用光滑的曲线顺次连结五个点)(1)列表(列出对图象形状起关键作用的五点坐标)(2)描点(定出五个关键点)x6yo--12345-2-3-41正弦曲线yxo1-122322思考:如何由的图象得到的图象?y=sinx，x[0,2]y=sinx，xRy=sinxx[0,2]y=sinxxRsin(x+2k)=sinx,kZ利用图象平移课本P32探究找出余弦函数的五个关键点，并用“五点法”作出y=cosx，x[0,2]的简图.二、余弦函数的图象与x轴的交点)0,0()0,()0,2(图象的最高点(,1)2图象的最低点)1-(,23与x轴的交点)0,(2)0,(23图象的最高点)1,0()1,2(图象的最低点)1,(sin[0,2]yxxcos[0,2]yxxxy1-1cossin()2yxx余弦曲线正弦曲线正弦曲线余弦函数的图象可以通过将正弦曲线余弦函数的图象可以通过将正弦曲线向左向左平行移动平行移动/2/2个单位长度而得到个单位长度而得到如何利用正弦函数y=sinx，xR图象作出余弦函数y=cosx，xR图象？思考三、典例分析例1画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-101o1yx22322-12y=sinx，x[0,2]y=1+sinx，x[0,2]2101向上平移1个单位长度列表解:描点连线思考：函数y=1+sinx的图象与函数y=sinx的图象有什么关系？例2画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]思考：函数y=-cosx的图象与函数y=cosx的图象有什么关系？关于x轴对称列表解:y=-sinx,x[0,]22y=sinx,x[0,]1-12322xy2拓展与提升:如何利用正弦函数的图像作出函数和函数的图像呢？2y=sinx，x[0,]y=-sinx，x[0,]2y=1–sinx，x[0,]209:21y=1-sinx,x[0,2]π1.正弦曲线、余弦曲线作法几何作图法（三角函数线）描点法（五点法）图象变换法yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]2.正弦曲线和余弦曲线之间的区别与联系。3.体会数形结合的思想。课堂小结课堂小结通过这节课的学习，同学们有什么收获？课后作业1.导学案的巩固作业2.课外查找单位圆中的三角函数线和三角函数的图象资料数与形数与形,,本是相倚依本是相倚依,,焉能分作两边飞焉能分作两边飞;;数无形时少直觉数无形时少直觉,,形少数时难入微形少数时难入微;;数形结合百般好数形结合百般好,,隔离分家万事休隔离分家万事休;;切莫忘切莫忘,,几何代数统一体几何代数统一体,,永远联系莫分永远联系莫分离离..——————华罗庚华罗庚