选修1-1导数的几何意义VIP免费

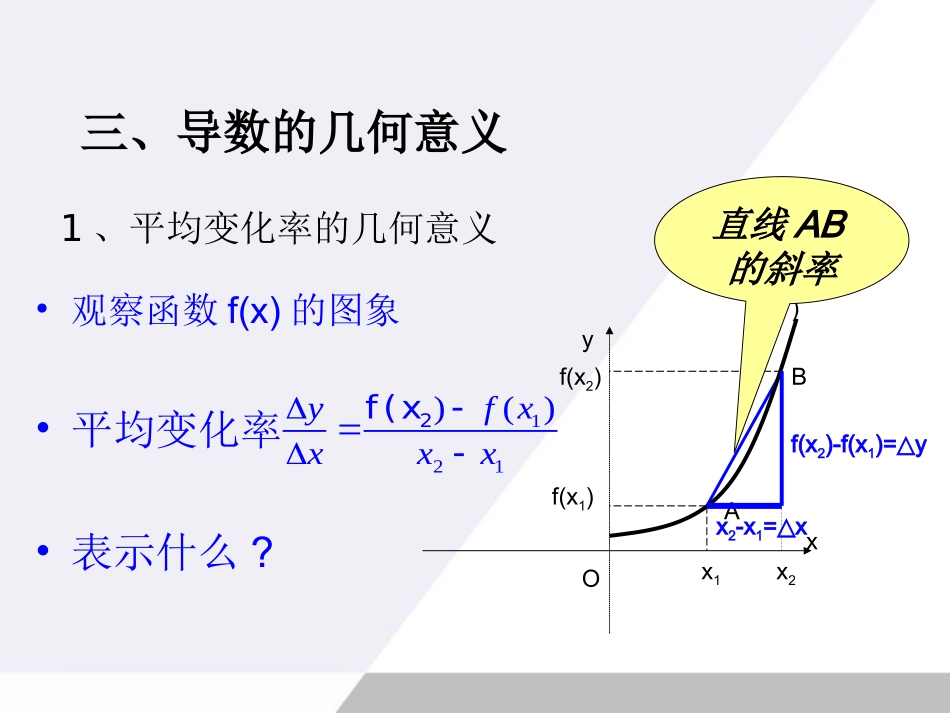
3.1.2《导数的几何意义》1.平均变化率0已知函数y=f(x)在点x=x及其附近有定义00叫做函数y=f(x)在x到x+x之间的平均变化率.00()()x0,fxxfxyxx当时比值'000)()()limxxfxfxx0f(x故00函数在x的瞬时变化率，就定义为f(x)在x=x处的导数0''0xxfxy记作或2.瞬时变化率00()()0fxxfxxx当趋近于时，平均变化率趋近于一个常数，这个常数称为函数在点的瞬时变化率fx0x复习回顾3.导数的定义•观察函数f(x)的图象•平均变化率•表示什么?121)()fxyxxx2f(xOABxyY=f(x)x1x2f(x1)f(x2)x2-x1=x△f(x2)-f(x1)=y△直线AB的斜率三、导数的几何意义1、平均变化率的几何意义βy=f(x)PQMΔxΔyOxyβPy=f(x)QMΔxΔyOxy如图,曲线C是函数y=f(x)的图象,P(x0,y0)是曲线C上的任意一点,Q(x0+Δx,y0+Δy)为P邻近一点,PQ为C的割线,PM//x轴,QM//y轴,β为PQ的倾斜角..tan,,:xyyMQxMP则.yx可见：就是割线的斜率观察：当点(n=1,2,3,4)沿着曲线f(x)趋近于点时，割线的变化趋势是什么？(,())nnnPxfx00(,())Pxfx结论：当趋近于点p时，割线趋近于确定位置的直线PT即点P处的切线nPnPP的斜率探究曲线的切线及切线的斜率探究曲线的切线及切线PQoxyy=f(x)割线切线T请看当点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况.我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.切线：当点趋近于点P时，直线趋近于确定的位置，这个确定位置的直线PT称点处的切线nPnPP这种切线定义适用于各种曲线思考：这里的切线定义与以前的切线定义有何不同？割线的极限位置就是切线割线切线T00,Pxfx00,Qxxfxxyxoxyyfx圆的切线定义并不适用于一般的曲线。通过逼近的方法，将割线趋于的确定位置的直线定义为切线（交点可能不惟一）适用于各种曲线。所以，这种定义才真正反映了切线的直观本质。2l1lxyABC函数在处的导数)(xf0xx就是函数的图象在点)(xf))(,(00xfxA斜率的切线PT的即:'00000()()()limlimxxfxxfxykfxxx切线这个概念:①提供了求曲线上某点切线的斜率的一种方法;00()(,())yfxMxfx曲线在点处000()()yyfxxx的切线方程为②切线斜率的本质—函数在处的导数.0xx0().yfxxx函数在处的切线的斜率就是函数在该点时的导数0().yfxxx函数在处的切线的斜率就是函数在该点时的导数例1:求抛物线y=f(x)=x2在点P(1,1)处的切线的斜率.'02020:(1)(1)1lim(1)1lim2()lim2.xxxfxffxxxxxx解过点(1,1)切线的斜率是（）2112.x因此，抛物线y=f=x在点P，处的切线斜率为2yxyxo1,1P例题讲解例2:求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.QPy=x2+1xy-111OMyx.2)(2lim)11(1)1(lim)()(lim:2020000xxxxxxxfxxfkxxx解因此,切线方程为y-2=2(x-1),即y=2x.求曲线在某点处的切线方程的基本步骤:先利用切线斜率的定义求出切线的斜率,然后利用点斜式求切线方程.处的切线方程为，在点）函数（)221(11xy处的切线方程为，在点）函数（)221(11xykAxxy斜率处的，，求曲线上点）已知（)21(322kAxxy斜率处的，，求曲线上点）已知（)21(322练习4x-y-4=06分析：求曲线在某点处的切线方程的基本步骤:①求出P点的坐标;②利用切线斜率的定义求出切线的斜率;③利用点斜式求切线方程.（3）已知2()2fxxx，求在处的切线方程．2x（1）求出函数在点x0处的导数即，得到曲线在点(x0,f(x0))的切线的斜率。)(0xf（2）根据直线方程的点斜式写出切线方程，即).)(()(000xxxfxfyd.求切线方程的步骤：小结:无限逼近的极限思想是建立导数概念、用导数定义求函数的导数的基本思想，丢掉极限思想就无法理解导数概念。/0()()()limxfxxfxfxx思考：这里的切线定义与以前的切线定义有何不同？割线的极限位置就是切线割线切线T00,Pxfx00,Qxxfxxyxoxyyfx圆的切线定...