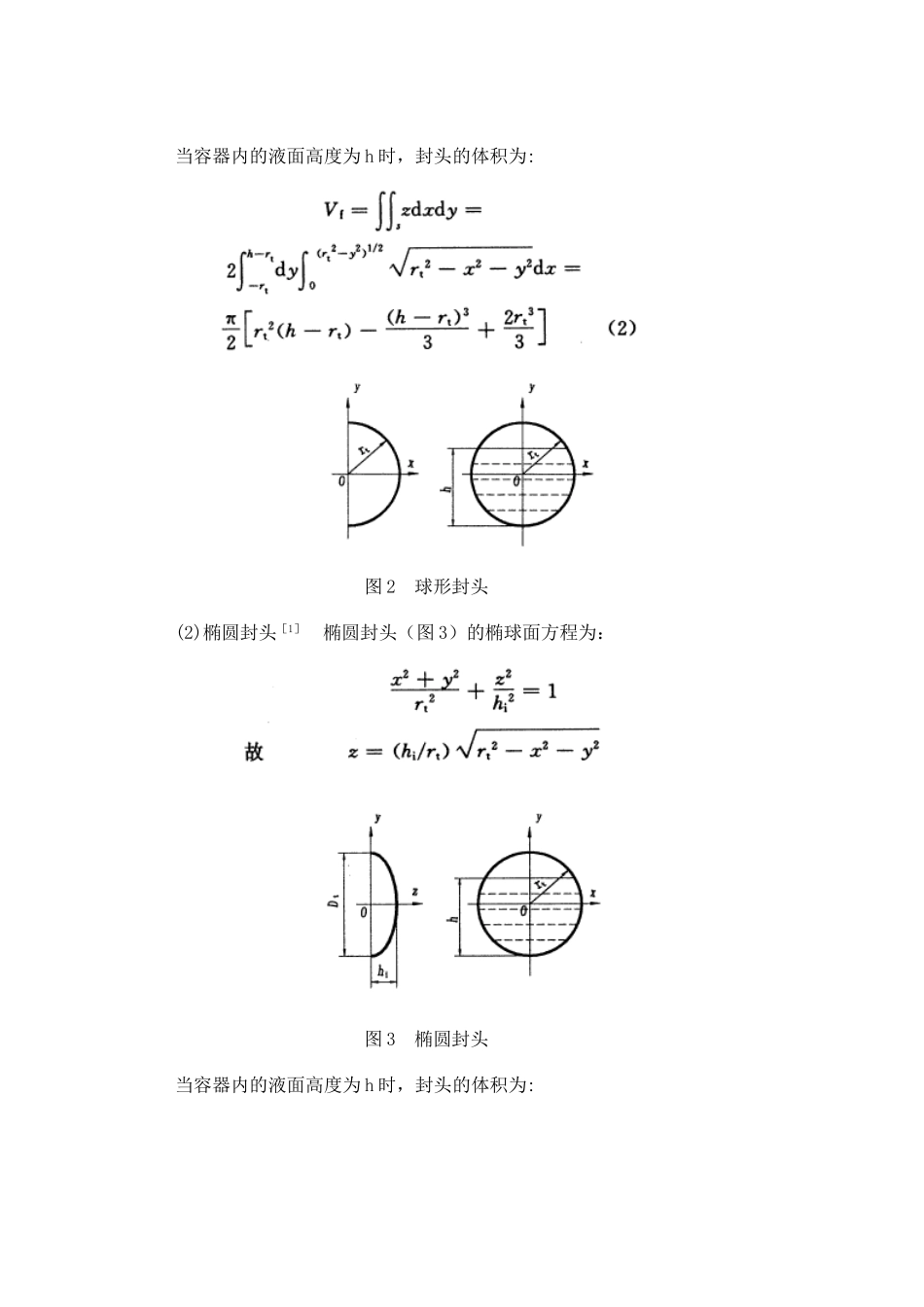
各种封头的卧式容器不同液面高度体积计算高炳军苏秀苹摘要:推导了各种封头形式的卧式容器不同液面高度的体积计算公式,编制了Quick-BASIC计算程序,可为卧式容器的设计和使用提供方便。关键词:封头;卧式容器;液面高度;体积;计算公式;程序中图分类号:TQ053.202文献标识码:AVolumecalculationofhorizontalvesselswithvariousformedheadsatdifferentliquidheightsGAOBing-jun,SUXiu-ping(HebeiUniversityofTechnology,Tianjin300130,China)Abstract:Volumecalculationformulaeofhorizontalvesselswithvariousformedheadsatdifferentliquidheightsarederived,Quick-BASICprogramisalsoworkedout.Itwillprovideconvenienceforthedesigningandusingofhorizontalvessels.Keywords:head;horizontalvessel;liquidheight;volume;calculationformula;program符号说明Dt——筒体内径,mmFK,FK+1——分别为各层积分区间划分个数为K和K+1时的体积计算值,m3h——液面高度,mmhi——封头曲面深度,mmh1,h2——分别为碟形封头球面与圆弧折边过渡处平行圆的最低和最高高度,mmL——筒体长度(含封头直边高度),mmR——封头球面内半径,mmr——碟形封头折边圆弧半径,mmrt——筒体或球形封头内半径,mmrs——碟形封头球面与圆弧折边过渡处平行圆半径,mmyr——碟形封头折边圆弧圆心与z轴的距离,mmzR——封头球面球心与y轴的距离,mmV——卧式容器体积,m3Vt——筒体部分体积,m3Vf——封头部分体积,m3在设计或者使用卧式容器时,常常要计算不同液面高度所对应的体积,有时还需要列出体积高度对照表或图。在一般资料中仅能查到容器总体积的计算公式,而要计算不同液面高度下的体积,则需要设计者或使用者自行推导公式计算,卧式容器的封头形式不同,则推导计算的难易程度也不同。球形封头和椭圆封头卧式容器较易推算,而无折边球形封头和碟形封头卧式容器的推算比较难,主要是推导计算中涉及到的积分运算难易不同,前2种比较容易得到解析解,而后2种比较难,只能利用计算机进行数值积分得到数值解。笔者推导了各种封头形式的卧式容器不同液面高度的体积计算公式,并编制了Quick-BASIC计算程序,可以为卧式容器的设计和使用提供方便。1计算公式1.1筒体筒体(图1)的横截面方程为:x2+y2=rt2故x=(rt2-y2)1/2液面高度为h时的体积为:图1筒体1.2封头(1)球形封头球形封头(图2)的球面方程为:x2+y2+z2=rt2故z=(rt2-x2-y2)1/2当容器内的液面高度为h时,封头的体积为:图2球形封头(2)椭圆封头[1]椭圆封头(图3)的椭球面方程为:图3椭圆封头当容器内的液面高度为h时,封头的体积为:(3)无折边球形封头无折边球形封头(图4)的球面方程为:x2+y2+(z+zR)2=R2故z=(R2-x2-y2)1/2-zR其中,R=(hi2+rt2)/(2hi),zR=(rt2-hi2)/(2hi)。当容器内的液面高度为h时,封头的体积为:实际上当hi=rt时,无折边球形封头即为球形封头。图4无折边球形封头(4)碟形封头碟形封头的曲面由半径为R的球面部分和圆弧半径为r的折边曲面部分组成,见图5,其球面方程为:x2+y2+(z+zR)2=R2故z=(rt2-x2-y2)1/2-zR其中,zR=[(R-r)2-(rt-r)2]1/2。圆弧半径为r的折边曲面方程为[2]:图5碟形封头其中,yr=rt-r。令h1=rt-rs,h2=rt+rs,其中,rs=R(rt-r)/(R-r),当容器内的液面高度为h,h≤h1时,封头的体积为:当容器内的液面高度为h,h1≤h≤h2时,封头的体积为:当容器内的液面高度为h,h>h2时,封头的体积为:1.3卧式容器卧式容器不同液面高度的体积为:V=Vt+2Vf(8)2电算程序从上面推导的计算公式来看,式(1)~(3)能直接计算,而式(4)~(7)所涉及的积分较为复杂,无法得出解析解,只能进行数值积分,为此笔者利用Quick-BASIC语言编制了电算程序,对式(1)~(8)进行计算,其中利用Gauss求积公式对式(4)~(7)进行双重积分,得出其近似数值解。Gauss型求积公式是数值积分方法中精度最高的一种,笔者采用8节点Gauss-Legendre求积公式,单层积分可达到17次代数精度,总体积分精度取决于各层积分的区间划分个数K,计算的终止条件可由控制参数EPS(EPS=|(FK+1-FK)/FK+1|)决定,Gauss型求积公式具体内容及Ga...