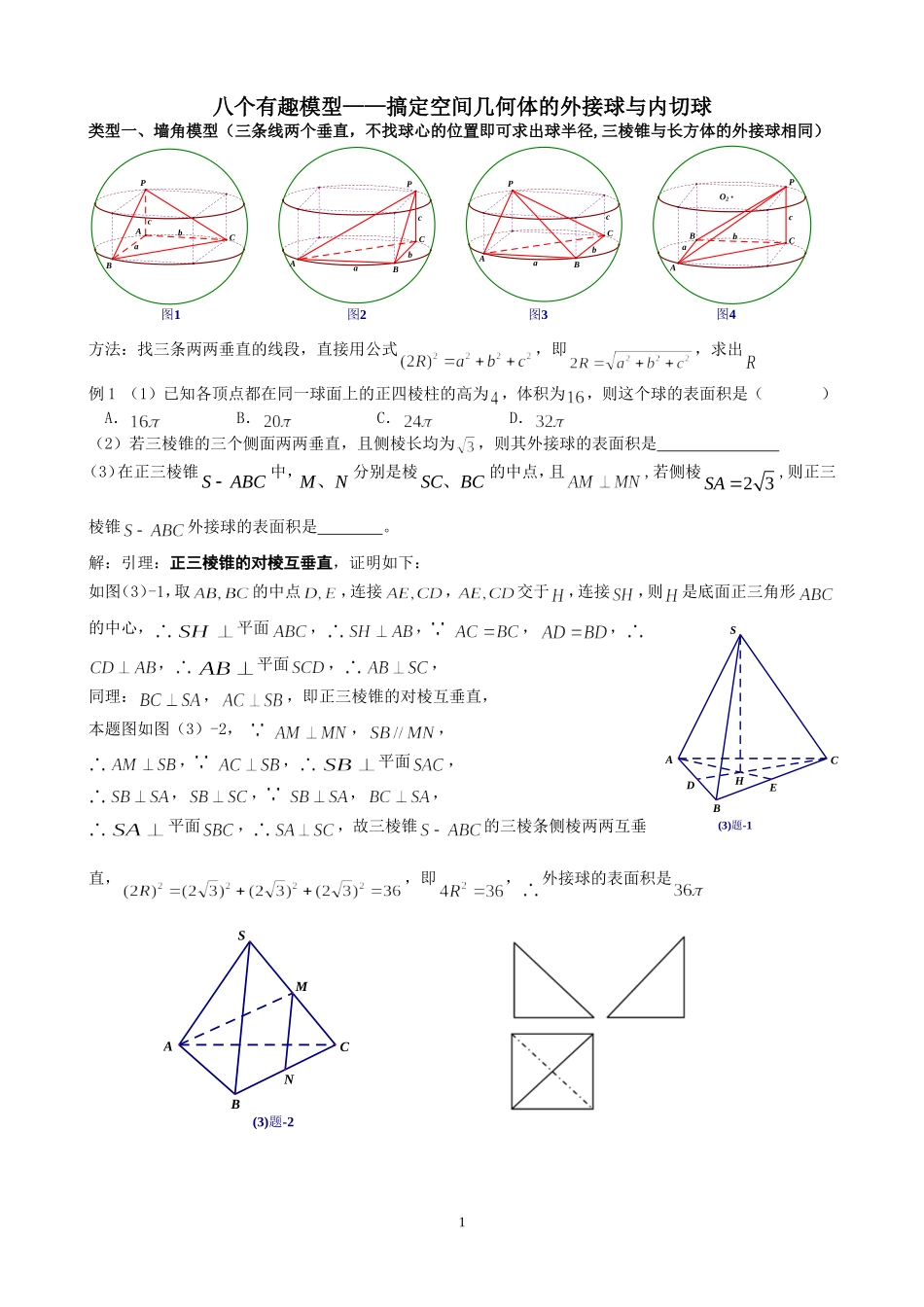
八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型(三条线两个垂直,不找球心的位置即可求出球半径,三棱锥与长方体的外接球相同)cab图1CPABabc图2PCBAabc图3CBPAabc图4PCO2BA方法:找三条两两垂直的线段,直接用公式,即,求出例1(1)已知各顶点都在同一球面上的正四棱柱的高为,体积为,则这个球的表面积是()A.B.C.D.(2)若三棱锥的三个侧面两两垂直,且侧棱长均为,则其外接球的表面积是(3)在正三棱锥SABC中,MN、分别是棱SCBC、的中点,且,若侧棱23SA,则正三棱锥外接球的表面积是。解:引理:正三棱锥的对棱互垂直,证明如下:如图(3)-1,取的中点,连接,交于,连接,则是底面正三角形的中心,平面,,,,,平面,,同理:,,即正三棱锥的对棱互垂直,本题图如图(3)-2,,,,,平面,,,,,平面,,故三棱锥的三棱条侧棱两两互垂直,,即,外接球的表面积是1(3)题-1HEDBACS(3)题-2MNABCS(4)在四面体SABC中,,则该四面体的外接球的表面积为()(5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是(6)已知某几何体的三视图如图上右所示,三视图是腰长为1的等腰直角三角形和边长为1的正方形,则该几何体外接球的体积为类型二、垂面模型(一条直线垂直于一个平面)1.题设:如图5,平面解题步骤:第一步:将画在小圆面上,为小圆直径的一个端点,作小圆的直径,连接,则必过球心;第二步:为的外心,所以平面,算出小圆的半径(三角形的外接圆直径算法:利用正弦定理,得),;第三步:利用勾股定理求三棱锥的外接球半径:①;②2.题设:如图6,7,8,的射影是的外心三棱锥的三条侧棱相等三2图5ADPO1OCB棱锥的底面在圆锥的底上,顶点点也是圆锥的顶点图6PADO1OCB图7-1PAO1OCB图7-2PAO1OCB图8PAO1OCB图8-1DPOO2ABC图8-2POO2ABC图8-3DPOO2AB解题步骤:第一步:确定球心的位置,取的外心,则三点共线;第二步:先算出小圆的半径,再算出棱锥的高(也是圆锥的高);第三步:勾股定理:,解出.方法二:小圆直径参与构造大圆。例2一个几何体的三视图如右图所示,则该几何体外接球的表面积为A.3B.2C.316D.以上都不对类型三、切瓜模型(两个平面互相垂直)图9-1ACBP图9-2AO1OCBP图9-3PAO1OCB图9-4AO1OCBP1.题设:如图9-1,平面平面,且(即为小圆的直径)第一步:易知球心必是的外心,即的外接圆是大圆,先求出小圆的直径;第二步:在中,可根据正弦定理,求出。32.如图9-2,平面平面,且(即为小圆的直径)3.如图9-3,平面平面,且(即为小圆的直径),且的射影是的外心三棱锥的三条侧棱相等三棱的底面在圆锥的底上,顶点点也是圆锥的顶点解题步骤:第一步:确定球心的位置,取的外心,则三点共线;第二步:先算出小圆的半径,再算出棱锥的高(也是圆锥的高);第三步:勾股定理:,解出4.如图9-3,平面平面,且(即为小圆的直径),且,则利用勾股定理求三棱锥的外接球半径:①;②例3(1)正四棱锥的顶点都在同一球面上,若该棱锥的高为1,底面边长为,则该球的表面积为。(2)正四棱锥的底面边长和各侧棱长都为,各顶点都在同一个球面上,则此球的体积为(3)在三棱锥中,,侧棱与底面所成的角为,则该三棱锥外接球的体积为()A.B.3C.4D.43(4)已知三棱锥SABC的所有顶点都在球O的求面上,ABC是边长为1的正三角形,SC为球O的直径,且2SC;则此棱锥的体积为()A.26B.36C.23D.22类型四、汉堡模型(直棱柱的外接球、圆柱的外接球)4图10-1C1B1AA1O1OO2BC图10-2C1B1AA1O1OO2BC图10-3C1B1AA1O1OO2BC题设:如图10-1,图10-2,图10-3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)第一步:确定球心的位置,是的外心,则平面;第二步:算出小圆的半径,(也是圆柱的高);第三步:勾股定理:,解出例4(1)一个正六棱柱的底面上正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为,底面周长为,则这个球的体积为(2)直三棱柱111ABCABC的各顶点都在同一球面上,若12ABACAA,120BAC,则此球...