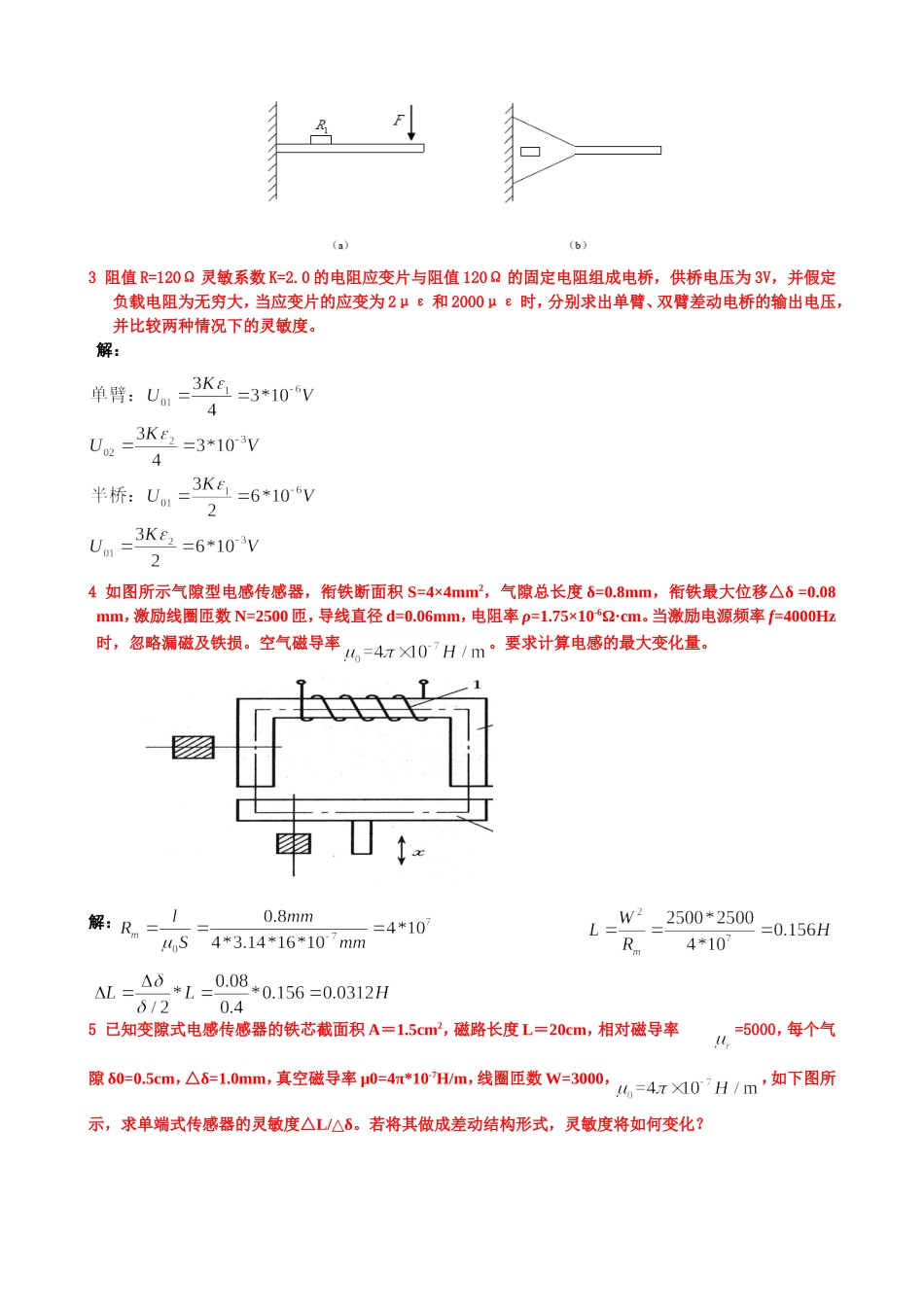
传感器计算题目总结第二章1一光电管与5kΩ电阻串联,若光电管的灵敏度为30µA/lm,试计算当输出电压为2V时的入射光通量。解:外光电效应所产生的电压为RL负载电阻,I光电流,入射光通量。K光电管的灵敏度,单位A/lm。入射光通量为2光敏二极管的光照特性曲线和应用电路如图所示,图中l为反相器,RL为20kΩ,求光照度为多少lx时Uo为高电平。【】解:当反相器的输入满足翻转条件时,反相器翻转,为高电平。现图中标明,所以必须小于2.5V,才能翻转为高电平。由于光敏二极管的伏安特性十分平坦,所以可以近似地用欧姆定律来计算与的关系。从图中可以看出光敏二极管的光照特性是线性的,所以根据比例运算得到时的光照度所以即光照度E必须大于时才为高电平。第四章1一热敏电阻在0℃和100℃时,电阻值分别为200kΩ和10kΩ。试计算该热敏电阻在20℃时的电阻值。2将一支灵敏度为0.08mv/0C的热电偶与电压表相连,电压表接线端处温度为500C,电压表读数为60mv,求热电偶热端温度?3用一K型热电偶测量温度,已知冷端温度为40℃,用高精度毫伏表测得此时的热电动势为29.186mV,求被测的热端温度大小?解:29.186+1.612=30.798mV热端温度为740℃第五章1图为一直流应变电桥,E=4V,R1=R2=R3=R4=350Ω,求:R1①为应变片其余为外接电阻,R1增量为△R1=3.5Ω时输出U0=?。R1②、R2是应变片,感受应变极性大小相同,其余为电阻,电压输出U0=?。R1③、R2感受应变极性相反,输出U0=?。R1④、R2、R3、R4都是应变片,对臂同性,邻臂异性,电压输出U0=?。2如图所示为等强度梁测力系统,R1为电阻应变片,应变片灵敏度系数k=2.05,未受应变时R1=120Ω,当试件受力F时,应变片承受平均应变ε=8×10−4,求(1)应变片电阻变化量ΔR1和电阻相对变化量ΔR1/R1。(2)将电阻应变片置于单臂测量电桥,电桥电源电压为直流3V,求电桥输出电压是多少。温度(℃)40739740741电势值(mV)1.61230.75730.79830.843阻值R=120Ω灵敏系数K=2.0的电阻应变片与阻值120Ω的固定电阻组成电桥,供桥电压为3V,并假定负载电阻为无穷大,当应变片的应变为2με和2000με时,分别求出单臂、双臂差动电桥的输出电压,并比较两种情况下的灵敏度。解:4如图所示气隙型电感传感器,衔铁断面积S=4×4mm2,气隙总长度δ=0.8mm,衔铁最大位移△δ=0.08mm,激励线圈匝数N=2500匝,导线直径d=0.06mm,电阻率ρ=1.75×10-6Ω·cm。当激励电源频率f=4000Hz时,忽略漏磁及铁损。空气磁导率。要求计算电感的最大变化量。解:5已知变隙式电感传感器的铁芯截面积A=1.5cm2,磁路长度L=20cm,相对磁导率=5000,每个气隙δ0=0.5cm,△δ=1.0mm,真空磁导率μ0=4π*10-7H/m,线圈匝数W=3000,,如下图所示,求单端式传感器的灵敏度△L/△δ。若将其做成差动结构形式,灵敏度将如何变化?解:灵敏度:如果做成差动形式,灵敏度加倍。灵敏度变为:34*2=686如图所示气隙型电感传感器,衔铁断面积S=4×4mm2,气隙总长度lδ=0.8mm,衔铁最大位移△lδ=0.08mm,激励线圈匝数N=2500匝,导线直径d=0.06mm,电阻率ρ=1.75×10-6Ω·cm。当激励电源频率f=4000Hz时,忽略漏磁及铁损。要求计算:(1)线圈电感值;(2)电感的最大变化量;(3)当线圈外断面积为11X11mm2时求其直流电阻值;(4)线圈的品质因数。解:(1)(2)当衔铁最大位移Δlδ=±0.08mm时,分别计算Δlδ=+0.08mm时电感L1为Δlδ=-0.08mm时电感L2为所以当衔铁最大位移变化±0.08mm时相应的电感变化量ΔL=L2-L1=65mH(3)线圈直流电阻式中lCP为线圈的平均每匝长度。根据铁心截面积4×4mm2及线圈外断面11×11mm2计算每匝总长度lCP=4×7.5=30mm。(4)线圈品质因数7下图为变极距型平板电容传感器的一种测量电路,其中CX为传感器电容,C为固定电容,假设运放增益A=∞,输入阻抗Z=∞;试推导输出电压U0与极板间距的关系,并分析其工作特点。将电容传感器接于放大器反馈回路,输入电路接固定电容。构成反相放大器。能克服变极距型传感器的非线性。由运算放大器工作原理可知,在开环放大倍数为-A和输入阻抗较大的情况下,有2.运算放大器式电路将电容传感器接于放大器反馈回路,输入电路接固定电容。构成反相放...