双曲线及其标准方程VIP免费

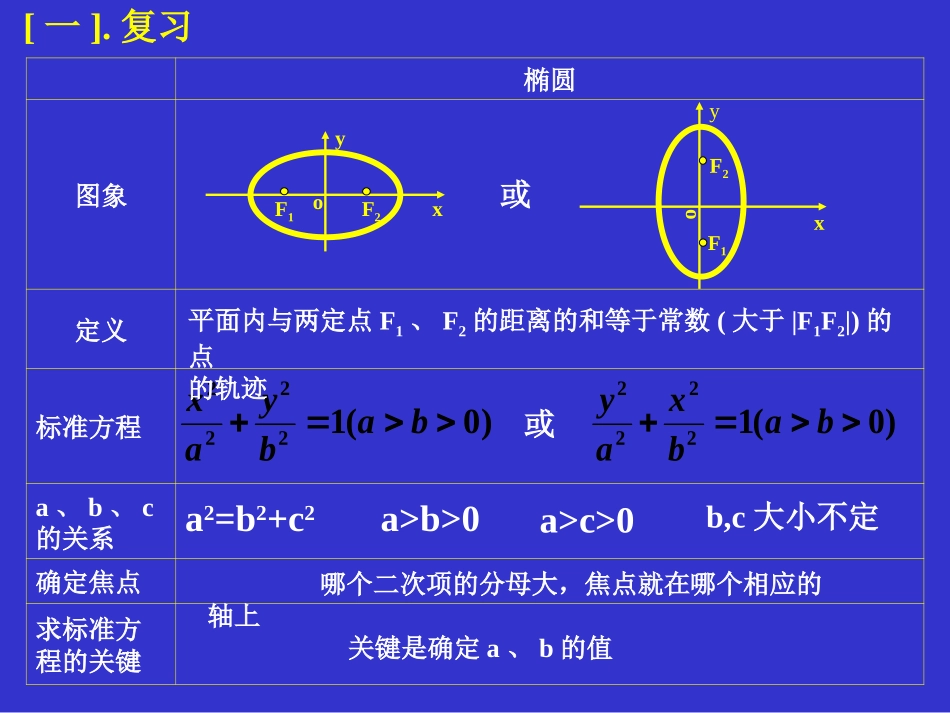
§8.3双曲线及其标准方程oxyoxyoxyoxyoxyoxyoxy[一].复习椭圆图象定义标准方程a、b、c的关系确定焦点求标准方程的关键)0(12222babyax平面内与两定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹yxF1F2o)0(12222babxaya2=b2+c2b,c大小不定a>b>0a>c>0哪个二次项的分母大，焦点就在哪个相应的轴上关键是确定a、b的值或oxyF1F2或[二]数学实验[1]取一条拉链，拉开一部分；[2]两边各取一个点，把它们固定在板上的两点F1、F2[3]把笔尖放在M点，随着拉链的拉开或者闭拢，笔尖画出一条的曲线。F1F2M？你能否根据刚才的实验给双曲线下个定义？[三].双曲线的定义平面内与两定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线F1F2M这两个定点F1、F2叫做双曲线的焦点两个焦点的距离叫做双曲线的焦距(1)建系设点设点M(x,y)在轨迹上则F1(-c,0),F2(c,0)，(2)写出点集P={M||MF1|-|MF2|=±2a}(3)列出方程[四]双曲线的标准方程221)(ycxMF222)(ycxMF因为所以aycxycx2)()(2222以线段F1F2的中点为原点，以F1F2所在的直线为x轴建立平面直角坐标系又设点M与F1、F2的距离的差的绝对值等于常数2aF1F2xyoM(x,y)移项后平方得aycxycx2)()(22222222222)()(44)(ycxycxaaycx(4)化简方程整理得：222)(ycxaacx两边平方得：2222222422222yacacxaxaacxaxcF1F2yxoM(x,y)整理得：)()(22222222acayaxac因为c>a,所以c2>a2，令c2-a2=b2则有：222222bayaxb两边同时除以a2b2得)0,0(12222babyaxF1F2yxoM(x,y)[四]双曲线的标准方程)0,0(12222babyax)0,0(12222babxay或yxF1F2oyxF1F2o练习1：不计算直接判断下列双曲线的焦点在那条轴上。1191622yx)(12362522xy)(1315822xy)(14112322yx)(结论：给出双曲线的标准方程，判断其焦点方法是：哪个二次项的系数为正，焦点就在哪个相应的轴上。[五]例题和练习例1.已知双曲线两个焦点的坐标为F1（-5，0）、F2（5，0），双曲线上一点P到F1、F2的距离的差的绝对值等于6，求双曲线的标准方程。解：因为双曲线的焦点在x轴上，所以设它的标准方程为：)0,0(12222babyax1635531026222222acbcaca,,：程为所求的双曲线的标准方116922yx结论：要求双曲线的标准方程关键是确定a、b的值。[六].小结双曲线图象定义标准方程a、b、c的关系确定焦点求标准方程的关键)0,0(12222babyax平面内与两定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹)0,0(12222babxayc2=a2+b2a、b大小不定c>a>0c>b>0哪个二次项的系数为正，焦点就在哪个相应的轴上关键是确定a、b的值或或yxF1F2ooxyF1F2练习2：根据下列条件，求双曲线的标准方程：（1）a=4,b=3,焦点在y轴上；（2）焦点的坐标是（-6，0），（6，0），并且经过点A（-5，2）解：（1）因为焦点在y轴上，所以设双曲线的标准方程为：12222bxay程为：所求的双曲线的标准方34ba,191622xy（2）因为焦点在x轴上，所以设双曲线的标准方程为：12222byax),(00ba),(00ba由双曲线的定义得：545556502650222222)()()()(a52a1620366222acbc又为：所求的双曲线标准方程1162022xy作业：课本P108习题8.3第1、3题。谢谢指导！