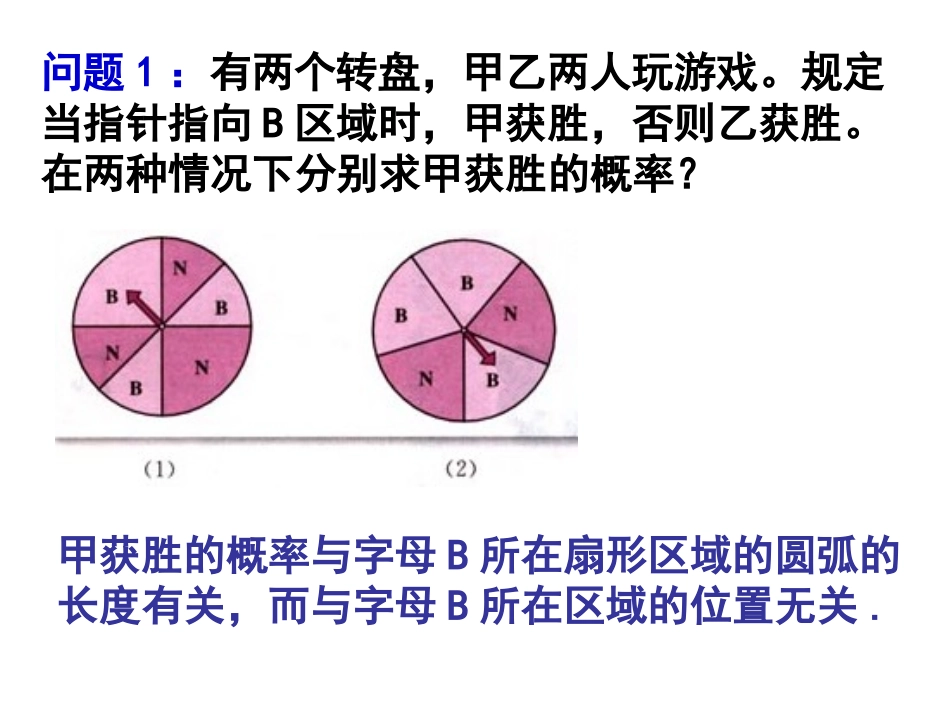
3.33.3几何概型几何概型11()APA包含基本事件的个数公式:基本事件的总数古典概型:特点:(1)试验中所有可能出现的基本事件只有有限个.(2)每个基本事件出现的可能性相等.返回问题1:有两个转盘,甲乙两人玩游戏。规定当指针指向B区域时,甲获胜,否则乙获胜。在两种情况下分别求甲获胜的概率?甲获胜的概率与字母B所在扇形区域的圆弧的长度有关,而与字母B所在区域的位置无关.问题2取一根长度为30cm的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于10cm的概率有多大?从30cm的绳子上的任意一点剪断.基本事件:31A)事件A发生的概率P(记“剪得两段绳长都不小于10cm”为事件A.把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生.由于中间一段的长度等于绳长的1/3.射中靶面直径为122cm的大圆内的任意一点.基本事件:问题3.射箭比赛的箭靶是涂有五个彩色的分环.从外向内为白色、黑色、蓝色、红色,靶心是金色,金色靶心叫“黄心”.奥运会的比赛靶面直径为122cm,靶心直径为12.2cm.运动员在70m外射箭,假设每箭都能中靶,且射中靶面内任一点都是等可能的,那么射中黄心的概率是多少?0.01122π4112.2π41(B)事件B发生的概率为P22事件B发生.的黄心内时,cm12.2π41而当中靶点落在面积为的大圆内,cm122π41为面积由于中靶点随机地落在黄心”为事件B,对于问题2.记“射中22223.AP(A)积)的区域长度(面积或体试验的全部结果所构成积)的区域长度(面积或体构成事件.AP(A)积)的区域长度(面积或体试验的全部结果所构成积)的区域长度(面积或体构成事件如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型。在几何概型中,事件A的概率的计算公式如下:与区域形状,位置无关,只于该区域大小有关下列概率模型中,是几何概型的有()(1)从区间[-10,10]内任取一个数,求取到1的概率(2)从区间[-10,10]内任取一个数,求取到绝对值不大于1的概率(3)从区间[-10,10]内任取一个整数,求取到大于1而小于2的概率(4)向一个边长为4cm的正方形ABCD内投一点P,求点P离中心不超过1cm的概率几何概型的判断例1.一张方桌的图案如图所示。将一颗豆子随机地扔到桌面上,假设豆子不落在线上,求下列事件的概率:(1)豆子落在红色区域;(2)豆子落在黄色区域;(3)豆子落在绿色区域;(4)豆子落在红色或绿色区域;(5)豆子落在黄色或绿色区域。例2、某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率。例2、某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率。打开收音机的时刻位于[50,60]时间段内则事件A发生.由几何概型的求概率公式得P(A)=(60-50)/60=1/6即“等待报时的时间不超过10分钟”的概率为1/6.解:设A={等待的时间不多于10分钟},打开收音机的时刻X是随机的,可以是0~60之间的任何一刻,并且是等可能的。称X服从[0,60]上的均匀分布,X为[0,60]上的随机数。1.有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率.2.如右下图,假设你在每个图形上随机撒一粒黄豆,分别计算它落到阴影部分的概率.练习:3:在数轴上,设点x∈[-3,3]中按均匀分布出现,记a∈(-1,2]为事件A,则P(A)=()A、1B、0C、1/2D、1/3C023-3-14.取一个边长为2a的正方形及其内切圆,随机向正方形内丢一粒豆子,求豆子落入圆内的概率.2a事件A,记“豆子落在圆内”为:解.4π豆子落入圆内的概率为答4π4aπa正方形面积圆的面积P(A)22