正弦、余弦函数的性质VIP免费

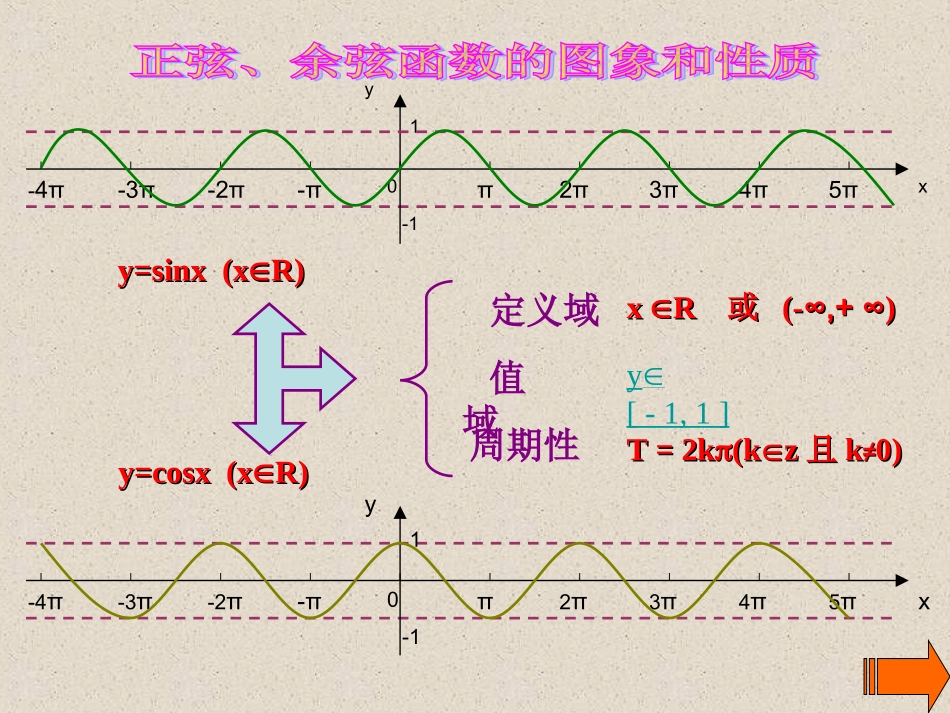
高中数学第一册(下)周期奇偶性单调性定义域值域0-π-2π-3π-4ππ2π3π4π5πxy-110-π-2π-3π-4ππ2π3π4π5πxy-11y=sinx(xy=sinx(xR)R)y=cosx(xy=cosx(xR)R)定义域值域周期性y[-1,1]T=2kT=2k(k(k∈∈zz且且kk≠≠0)0)xxRR或或(-(-∞,+∞∞,+∞))其中正弦函数y=sinx,xy=sinx,xRR(1)(1)当且仅当当且仅当x=+x=+2kπ,kz∈时,取得最大值1.(2)(2)当且仅当当且仅当x=-+x=-+2kπ,kz∈时,取得最大值-1.2π2而正弦函数y=cosx,xy=cosx,xRR(1)(1)当且仅当当且仅当x=x=2kπ,kz∈时,取得最大值1.(2)(2)当且仅当当且仅当x=(x=(2k+1)π,kz∈时,取得最大值-1.0-π-2π-3π-4ππ2π3π4π5πxy-11y=sinx(xy=sinx(xR)R)是奇函数sin(-x)=-sinxsin(-x)=-sinx(xR)y=cosx(xy=cosx(xR)R)是偶函数cos(-x)=cosx(xcos(-x)=cosx(xR)R)0-π-2π-3π-4ππ2π3π4π5πxy-11正弦函数图像关于原点对称正弦函数图像关于原点对称余弦函数图像关于y轴对称y=sinxyxo--12-2-3122322325y=sinx(xR)图象关于原点对称25327427-4223-π-2π253ππ2232π4π2527-3π0xy1-1xsinx20…2………23π-1010-1y=sinx(xR)减区间为[，]其值从1减至-1223???增区间为[，]其值从-1增至122223-π-2π253ππ2232π4π2527-3π0xy1-1xsinx20…2………23π-1010-1y=sinx(xR)减区间为[+2kπ，+2kπ]其值从1减至-1223增区间为[+2kπ，+2kπ]其值从-1增至122xsinx20…2………23π-1010-1y=cosx(xR)减区间为[2kπ，2kπ+π]其值从1减至-1增区间为[-π+2kπ,2kπ]其值从-1增至1223-π-2π253ππ2232π4π2527-3π0xy1-1例1:求使下列函数取得最大值的自变量x的集合,并说出最大值是什么?(1)y=cosx+1,xR(2)y=sin2x,xR解:使函数y=cosx+1,xR取得最大值的x的集合,就是使函数y=cosx,xR取得最大值的的集合{x|x=2kπ,kZ},所以函数y=cosx+1,xR的最大值是1+1=2。解:令Z=2x,那xR必须并且只需ZR,且使函数y=sinZ,ZR取得最大值的Z的集合是{Z|Z=+2kπ,kZ},由2x=Z=+2kπ,得x=+kπ即:使函数y=sin2x,x∈R取得最大值的x的集合是{x|x=+kπ,kZ},所以函数y=sin2x,x∈R的最大值是12424例2:求函数y=-cosx的单调区间解:由y=-cosx的图象可知:单调增区间为[2kπ,(2k+1)π](kz)单调减区间为[(2k-1)π,2kπ](kz)y1-1-2πx02-π2π23y=-cosx一、求下列函数的定义域：（1）y=1+xsin1xcos（2）y=二、函数是偶函数，则的一个值为_____)21sin(xyA.B.C.D.842三、f(x)是偶函数，x≥0时，f(x)=x-1(1)x<0时，f(x)=__________(2)f(x-1)<0的解集为__________小结小结奇偶性单调性（单调区间）奇函数偶函数[+2k2k,+2k2k],kZ22单调递增[+2k2k,+2k2k],kZ223单调递减[+2k2k,2k2k],kZ单调递增[2k2k,2k2k+],kZ单调递减函数余弦函数余弦函数正弦函数正弦函数求函数的单调区间：1.直接利用相关性质2.复合函数的单调性3.利用图象寻找单调区间