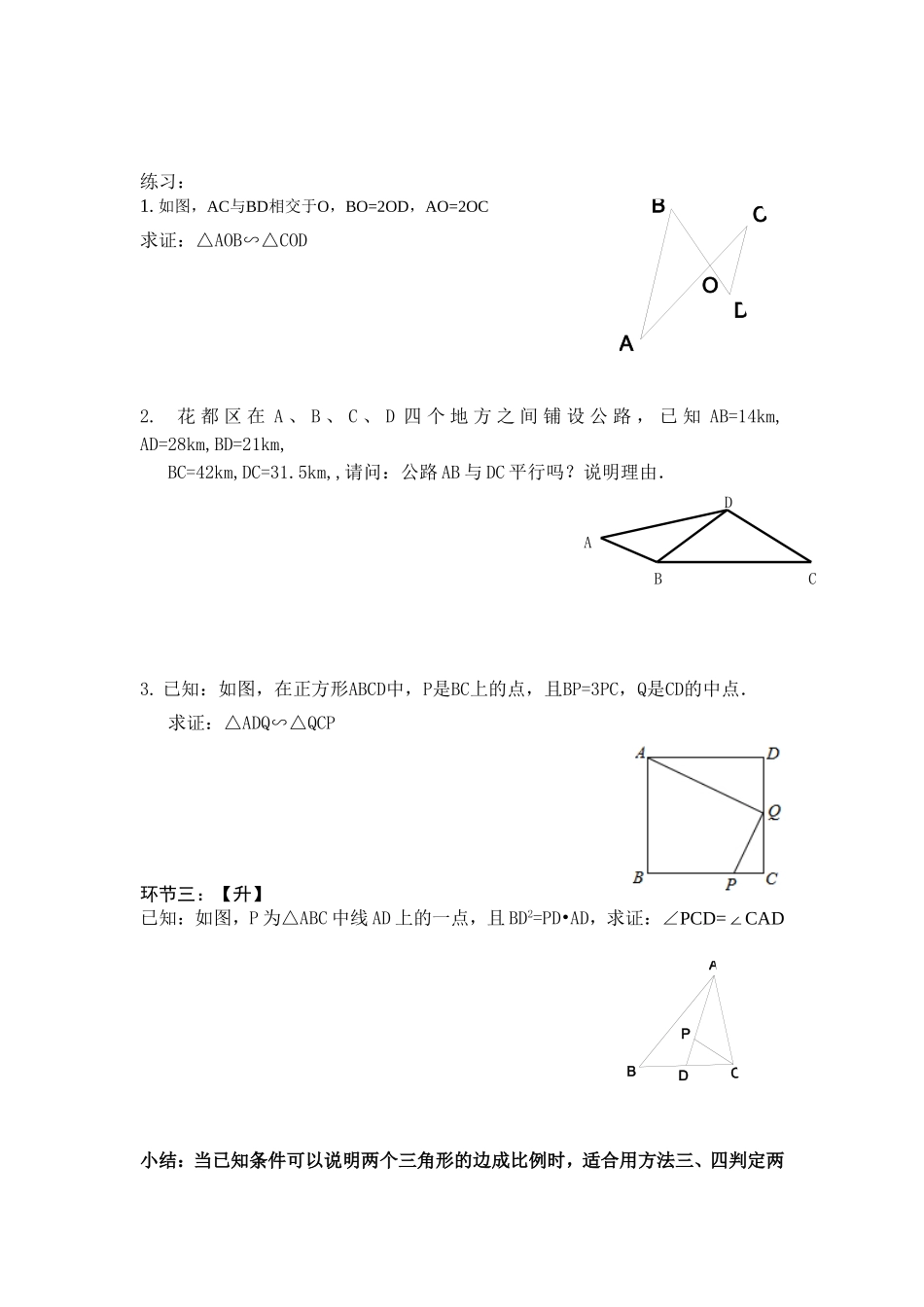
第二十七章《相似》第4课时相似三角形的判定(2)学习目标:会利用“两边成比例且夹角相等的两个三角形相似”(“SAS”)和“三边成比例的两个三角形相似”(“SSS”)的判定方法判定两个三角形相似环节一:【学】问题情景:1.两个三角形全等和三角形相似有什么关系?2.两个三角形全等的判定方法中有“SSS”和“SAS”,能否把这两种方法迁移到判定三角形相似,思考一下,需要做什么改变?猜想1:在△ABC和△A′B′C′中,则△ABC∽△A′B′C′猜想2:在△ABC和△A′B′C′中,∠B=∠B′则△ABC∽△A′B′C′上述两个猜想都可以证明,有兴趣的同学可以阅读书本P32有关的证明过程环节二:【导】归纳:相似判定方法三:三边成比例的两个三角形相似推理形式:∵∴△ABC∽△A′B′C′相似判定方法四:两边成比例且夹角相等的两个三角形相似推理形式:∵∠B=∠B′∴△ABC∽△A′B′C′练习:根据下列各组条件,判断△ABC和△A′B′C′是否相似,并说明理由.(1)∠A=40°,AB=8㎝,AC=15㎝;∠A′=40°,A′B′=16㎝,A′C′=30㎝(2)AB=12,BC=15,AC=24;A′B′=20,B′C′=25,A′C′=40例.B'C'A'ABCB'C'A'ABC,如图已知AEACDEBCADAB试说明∠1=2∠OCDABPCDBA练习:1.如图,AC与BD相交于O,BO=2OD,AO=2OC求证:△AOB∽△COD2.花都区在A、B、C、D四个地方之间铺设公路,已知AB=14km,AD=28km,BD=21km,BC=42km,DC=31.5km,,请问:公路AB与DC平行吗?说明理由.3.已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.求证:△ADQ∽△QCP环节三:【升】已知:如图,P为△ABC中线AD上的一点,且BD2=PD•AD,求证:∠PCD=∠CAD小结:当已知条件可以说明两个三角形的边成比例时,适合用方法三、四判定两ABCD个三角形相似.作业:1.课本P34页:练习第2题2.《导学案》P154:第1、3题和P155第5、6题