高二数学单元复习 知识精讲 人教版VIP免费

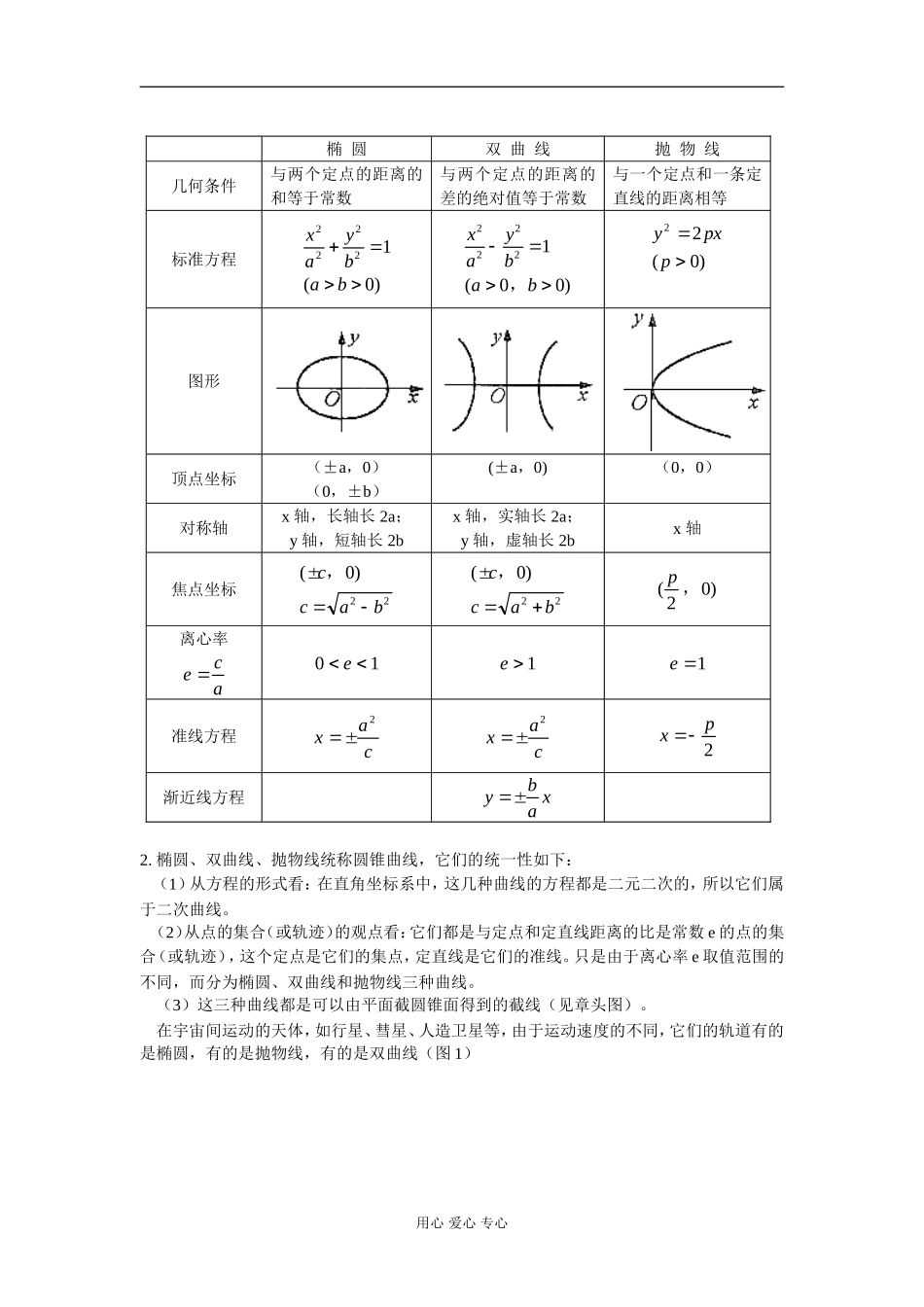
高二数学单元复习知识精讲人教版一.本周教学内容：单元复习【教学目标】1.理解并掌握椭圆、双曲线、抛物线的定义，并会应用于解题过程中；2.理解并掌握椭圆，双曲线，抛物线的标准方程及几何性质，并会应用。【能力训练】掌握求轨迹的常用方法——直译法、定义法、中间变量法；熟练掌握待定系数法求圆锥曲线的方程，进一步巩固数形结合的思想方法，落实坐标法及方程思想。【教学过程】一.知识结构圆锥曲线椭圆椭圆的定义标准方程几何性质第二定义双曲线双曲线的定义标准方程几何性质抛物线综合应用第二定义几何性质标准方程抛物线定义统一定义二.思想方法总结1.待定系数法是求椭圆、双曲线、抛物线方程的一个基本方法。2.直线和圆锥曲线的位置关系，可转化为直线和圆锥曲线的方程的公共解问题，体现了方程的思想。数形结合也是解决直线和圆锥曲线位置关系的常用方法。3.一些最值问题常用函数思想，运用韦达定理求弦的中点和弦长问题，是经常使用的方法。4.坐标法是研究曲线的重要方法，学会如何利用曲线的方程讨论曲线的几何性质，以及用坐标法证明简单的几何问题等。三.重点知识提要1.椭圆、双曲线、抛物线的标准方程（各取其中一种）和图形、性质如下表：）用心爱心专心椭圆双曲线抛物线几何条件与两个定点的距离的和等于常数与两个定点的距离的差的绝对值等于常数与一个定点和一条定直线的距离相等标准方程xaybab222210()xaybab2222100()，ypxp220()图形顶点坐标（±a，0）（0，±b）(±a，0)（0，0）对称轴x轴，长轴长2a；y轴，短轴长2bx轴，实轴长2a；y轴，虚轴长2bx轴焦点坐标()ccab，022()ccab，022()p20，离心率eca01ee1e1准线方程xac2xac2xp2渐近线方程ybax2.椭圆、双曲线、抛物线统称圆锥曲线，它们的统一性如下：（1）从方程的形式看：在直角坐标系中，这几种曲线的方程都是二元二次的，所以它们属于二次曲线。（2）从点的集合（或轨迹）的观点看：它们都是与定点和定直线距离的比是常数e的点的集合（或轨迹），这个定点是它们的集点，定直线是它们的准线。只是由于离心率e取值范围的不同，而分为椭圆、双曲线和抛物线三种曲线。（3）这三种曲线都是可以由平面截圆锥面得到的截线（见章头图）。在宇宙间运动的天体，如行星、彗星、人造卫星等，由于运动速度的不同，它们的轨道有的是椭圆，有的是抛物线，有的是双曲线（图1）用心爱心专心图1四.例题分析：例1.选择题：11003611022.椭圆上的点到它的左准线的距离是，那么点到它右焦点的xyPP距离为（）A.15B.12C.10D.82.已知A（0，-5），B（0，5），|PA|-|PB|=2a，当a=3和5时，点P的轨迹为（）A.双曲线和一条直线；B.双曲线和两条射线；C.双曲线一支和一条直线；D.双曲线一支和一条射线。317522221212.,设点为双曲线上一点，、为它的焦点，如果PxaybFFPFFPFF2115，则双曲线的离心率为（）ABCD....43362234202112233.(,)(,)(,)抛物线，（）上有，，三点，是它ypxpAxyBxyCxyF的焦点，若|AF|，|BF|，|CF|成等差数列，则（）A.x1，x2，x3成等差数列；B.y1，y2，y3成等差数列；C.x1，x3，x2成等差数列；D.y1，y3，y2成等差数列。解：1106845.,,,由椭圆方程知：abceca由椭圆第二定义||||PFPF1110458由椭圆第一定义||||||PFPFaPF12222012点到它的右焦点的距离为，选（）。PB12解：2.双曲线第一定义：平面内：动点M，定点F1，F2，若||MF1|-|MF2||=2a（1）当2a<|F1F2|时，动点M的轨迹是双曲线。（2）当2a=|F1F2|时，动点M的轨迹是两条射线。（3）当2a>|F1F2|时，动点没有轨迹。用心爱心专心特别：|MF1|-|MF2|=2a，且（1）成立时，为右一支|MF2|-|MF1|=2a，且（1）成立时，为左一支210326caa，时，22acP，点轨迹为上一支aaacP521022时，，，点轨迹为一条射线。选（）。D解：3.设|PF1|=m，|PF2|=nncmc275215sinsin，nmca275152(sinsin)caC175152sinsin，选。yPnmxF1F275°解：4.由抛物线定义：|AF|=|AA′|BFBBCFCC''2||||||BFAFCF...