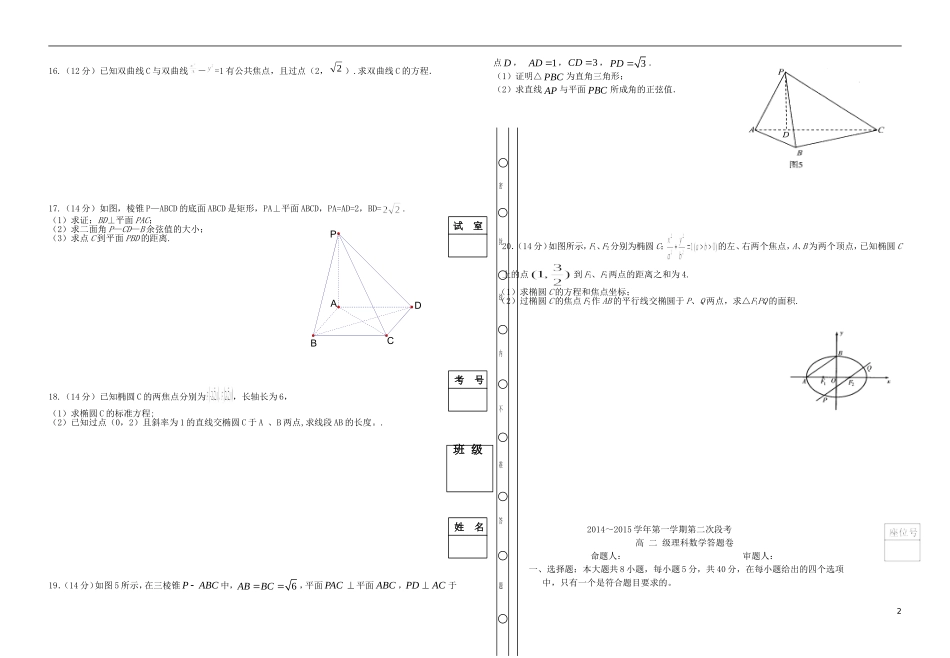
2014~2015学年度第一学期第二次段考高二级理科数学试题卷命题人:审题人:一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一个是符合题目要求的。1.若直线a与平面不垂直,那么平面内与直线a垂直的直线有()A.0条B.无数条C.0条或无数条D.不确定2.双曲线2x2-y2=8的实轴长是()A.2B.2C.4D.43.如果一个椭圆的长轴长是短轴长的两倍,那么这个椭圆的离心率为()A.45B.23C.22D.214.过点(3,2),且平行于直线的直线方程为()A.B.C.D.5.圆心为(-1,1),半径为2的圆的方程是()A.B.C.D.6.已知点Pab,(0ab)是圆O:222xyr内一点,直线l的方程为20axbyr,那么直线l与圆O的位置关系是()A.相离B.相切C.相交D.不确定7.曲线与曲线的()A.焦距相等B.焦点相同C.离心率相等D.以上都不对8.已知△ABC的周长为20,且顶点B(0,-4),C(0,4),则顶点A的轨迹方程是()A.(x≠0)B.(x≠0)C.(x≠0)D.(x≠0)二、填空题:本大题共6小题,每小题5分,共30分,将正确答案填在题中横线上。9.直线的倾斜角为10.经过两条直线和的交点,且垂直于直线的直线方程为11.双曲线的渐近线方程是12.如果方程x2+ky2=2表示焦点在y轴的椭圆,那么实数k的取值范围是____________.13.若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为14.如图,四棱锥S-ABCD的底面为正方形,SD底面ABCD,给出下列结论:①ACSB②AB//平面SCD③SA与平面ABD所成的角等于SC与平面ABD所成的角④ACSO⑤AB与SC所成的角等于DC与SA所成的角其中,正确结论的序号是三、解答题:(共6大题,共计80分)解答应写出文字说明,证明过程或演算步骤.15.(12分)已知圆C:,直线:。(1)当a为何值时,直线与圆C相切;(2)当直线与圆C相交于A、B两点,且时,求直线的方程。1ODCBAS16.(12分)已知双曲线C与双曲线-=1有公共焦点,且过点(2,2).求双曲线C的方程.17.(14分)如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=.(1)求证:BD⊥平面PAC;(2)求二面角P—CD—B余弦值的大小;(3)求点C到平面PBD的距离.18.(14分)已知椭圆C的两焦点分别为,长轴长为6,(1)求椭圆C的标准方程;(2)已知过点(0,2)且斜率为1的直线交椭圆C于A、B两点,求线段AB的长度。.19.(14分)如图5所示,在三棱锥ABCP中,6ABBC,平面PAC平面ABC,ACPD于点D,1AD,3CD,3PD.(1)证明△PBC为直角三角形;(2)求直线AP与平面PBC所成角的正弦值.20.(14分)如图所示,F1、F2分别为椭圆C:的左、右两个焦点,A、B为两个顶点,已知椭圆C上的点到F1、F2两点的距离之和为4.(1)求椭圆C的方程和焦点坐标;(2)过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点,求△F1PQ的面积.2014~2015学年第一学期第二次段考高二级理科数学答题卷命题人:审题人:一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一个是符合题目要求的。2试室密封线内不准答题姓名考号班级PDBCA二、填空题:本大题共4小题,每小题5分,共20分,将正确答案填在题中横线上。9.10.11.12.13.14.三、解答题:(共6大题,共计80分)解答应写出文字说明,证明过程或演算步骤.15.(12分)已知圆C:,直线:。(1)当a为何值时,直线与圆C相切;(2)当直线与圆C相交于A、B两点,且时,求直线的方程。16.(12分)已知双曲线C与双曲线-=1有公共焦点,且过点(2,2).求双曲线C的方程.17.(14分)如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=.(1)求证:BD⊥平面PAC;(2)求二面角P—CD—B余弦值的大小;(3)求点C到平面PBD的距离.18.(14分)已知椭圆C的两焦点分别为,长轴长为6,(1)求椭圆C的标准方程;(2)已知过点(0,2)且斜率为1的直线交椭圆C于A、B两点,求线段AB的长度。.题号12345678答案3PDBCA19.(14分)如图5所示,在三棱锥ABCP中,6ABBC,平面PAC平面ABC,ACPD于点D,1AD,3CD,3PD.(1)证明△PBC为直角三角形;(2)求直线AP与平面PBC所成角的正弦值.20.(14分)如图所示,F1、F2分别为椭圆C:的...