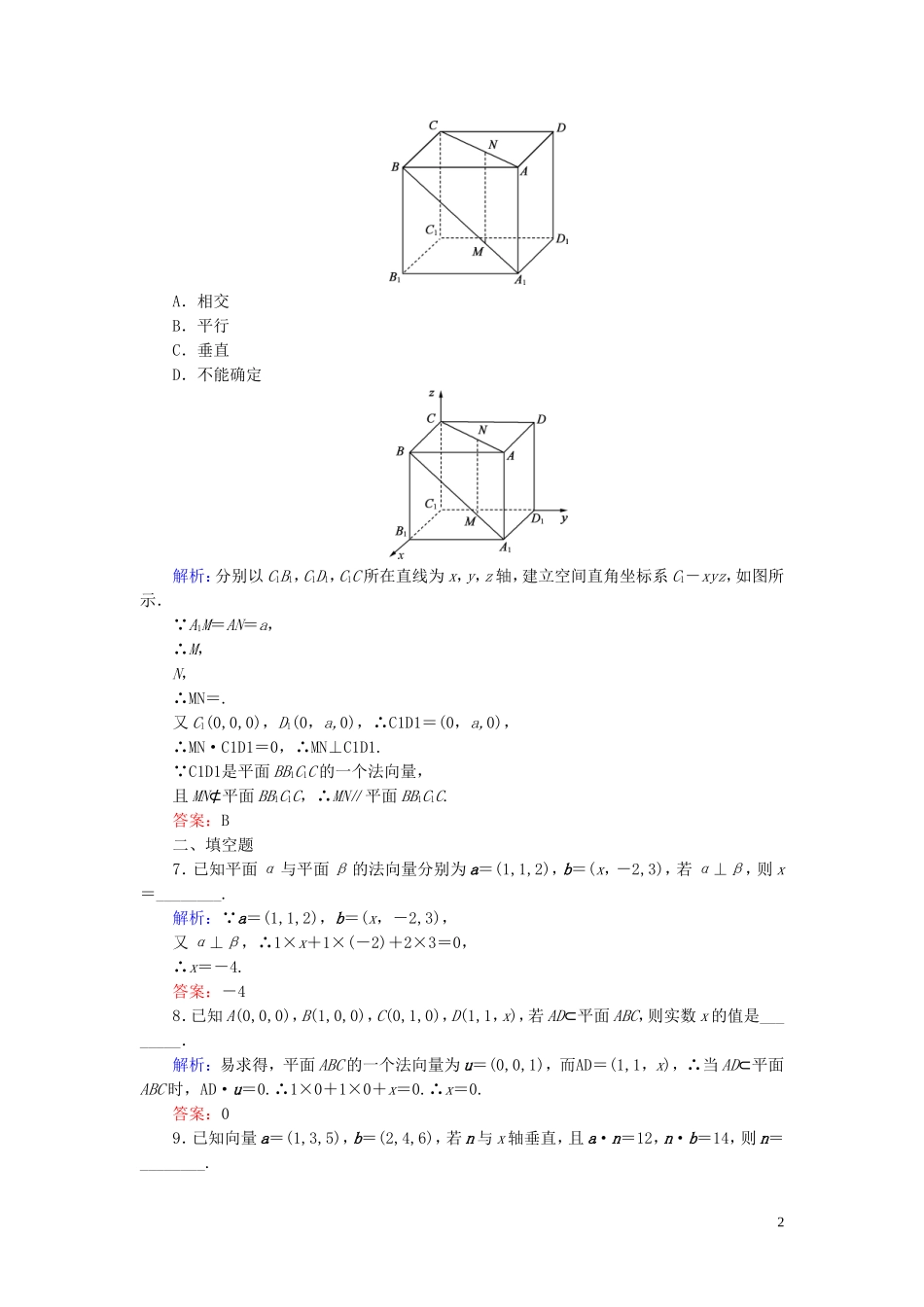
第一课时用空间向量解决平行关系课时跟踪检测一、选择题1.给定下列命题:①若n1,n2分别是平面α,β的法向量,则n1∥n2⇔α∥β;②若n1,n2分别是平面α,β的法向量,则α∥β⇔n1·n2=0;③若n是平面α的法向量,且向量a与平面α共面,则a·n=0;④若两个平面的法向量不垂直,则这两个平面一定不垂直.其中正确命题的个数是()A.1B.2C.3D.4解析:①③④正确.②中由α∥β⇒n1∥n2.答案:C2.已知平面α内有一个点A(2,-1,2),α的一个法向量为n=(3,1,2),则下列点P中,在平面α内的是()A.(1,-1,1)B.1,3,C.1,-3,D.-1,3,-解析:对于B,AP=-1,4,-,则n·AP=(3,1,2)·-1,4,-=0,∴n⊥AP,则点P1,3,在平面α内.答案:B3.若空间中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的关系为()A.平行B.垂直C.相交但不垂直D.无法确定解析:AB=(-2,-2,2),CD=(1,1,-1).故AB=-2CD.所以AB∥CD,即AB与CD平行.答案:A4.直线l的方向向量为a,平面α内两共点向量为OA,OB,下列关系中能表示l∥α的是()A.a=OAB.a=kOBC.a=λOA+μOBD.以上均可能解析:A,B,C均能表示l∥α或l⊂α.答案:D5.已知直线l过点P(1,0,-1),平行于向量a=(2,1,1),平面α过直线l与点M(1,2,3),则平面α的法向量不可能是()A.(1,-4,2)B.C.D.(0,-1,1)解析:解法一:由已知,得PM=(0,2,4),设平面α的法向量为n=(x,y,z),则有即把四个选项代入验证知,D项(0,-1,1)不满足.解法二:因为A,B,C中各向量平行,故选D.答案:D6.如图,在正方体ABCD-A1B1C1D1中,棱长为a,M,N分别为A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是()1A.相交B.平行C.垂直D.不能确定解析:分别以C1B1,C1D1,C1C所在直线为x,y,z轴,建立空间直角坐标系C1-xyz,如图所示. A1M=AN=a,∴M,N,∴MN=.又C1(0,0,0),D1(0,a,0),∴C1D1=(0,a,0),∴MN·C1D1=0,∴MN⊥C1D1. C1D1是平面BB1C1C的一个法向量,且MN⊄平面BB1C1C,∴MN∥平面BB1C1C.答案:B二、填空题7.已知平面α与平面β的法向量分别为a=(1,1,2),b=(x,-2,3),若α⊥β,则x=________.解析: a=(1,1,2),b=(x,-2,3),又α⊥β,∴1×x+1×(-2)+2×3=0,∴x=-4.答案:-48.已知A(0,0,0),B(1,0,0),C(0,1,0),D(1,1,x),若AD⊂平面ABC,则实数x的值是________.解析:易求得,平面ABC的一个法向量为u=(0,0,1),而AD=(1,1,x),∴当AD⊂平面ABC时,AD·u=0.∴1×0+1×0+x=0.∴x=0.答案:09.已知向量a=(1,3,5),b=(2,4,6),若n与x轴垂直,且a·n=12,n·b=14,则n=________.2解析:设n=(x,y,z),由题意,得得∴n=(0,-1,3).答案:(0,-1,3)三、解答题10.(2019·黑龙江实验中学期末)四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=PD.(1)证明:平面PQC⊥平面DCQ;(2)证明:PC∥平面BAQ.证明:如图,以D为坐标原点,线段DA的长为单位长度,DA为x轴的正方向建立空间直角坐标系D-xyz.(1)依题意,有Q(1,1,0),C(0,0,1),P(0,2,0),则DQ=(1,1,0),DC=(0,0,1),PQ=(1,-1,0),所以PQ·DQ=0,PQ·DC=0,即PQ⊥DQ,PQ⊥DC,且DQ∩DC=D.故PQ⊥平面DCQ.又PQ⊂平面PQC,所以平面PQC⊥平面DCQ.(2)根据题意,DA=(1,0,0),AB=(0,0,1),AQ=(0,1,0),故有DA·AB=0,DA·AQ=0,所以DA为平面BAQ的一个法向量.又因为PC=(0,-2,1),且DA·PC=0,即DA⊥PC,且PC⊄平面BAQ,故有PC∥平面BAQ.11.在正方体ABCD-A1B1C1D1中,求证:平面A1BD∥平面CB1D1.证明:以D为原点,分别以DA,DC,DD1所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系D-xyz,设正方体的棱长为1.则A1(1,0,1)、B(1,1,0)、D1(0,0,1)、B1(1,1,1)、C(0,1,0),∴A1D=(-1,0,-1),A1B=(0,1,-1),D1B1=(1,1,0),D1C=(0,1,-1),设平面A1DB的法向量为n1=(x1,y1,z1),则⇒令z1=1,得x1=-1,y1=1.∴平面A1DB的一个法向量为n1=(-1,1,1).设平面CB1D1的法向量为n2=(x2,y2,z2),则⇒令y2=1,得x2=-1,z2=1,∴n2=(-1,1,1).3∴n1=n2,即n1∥n...