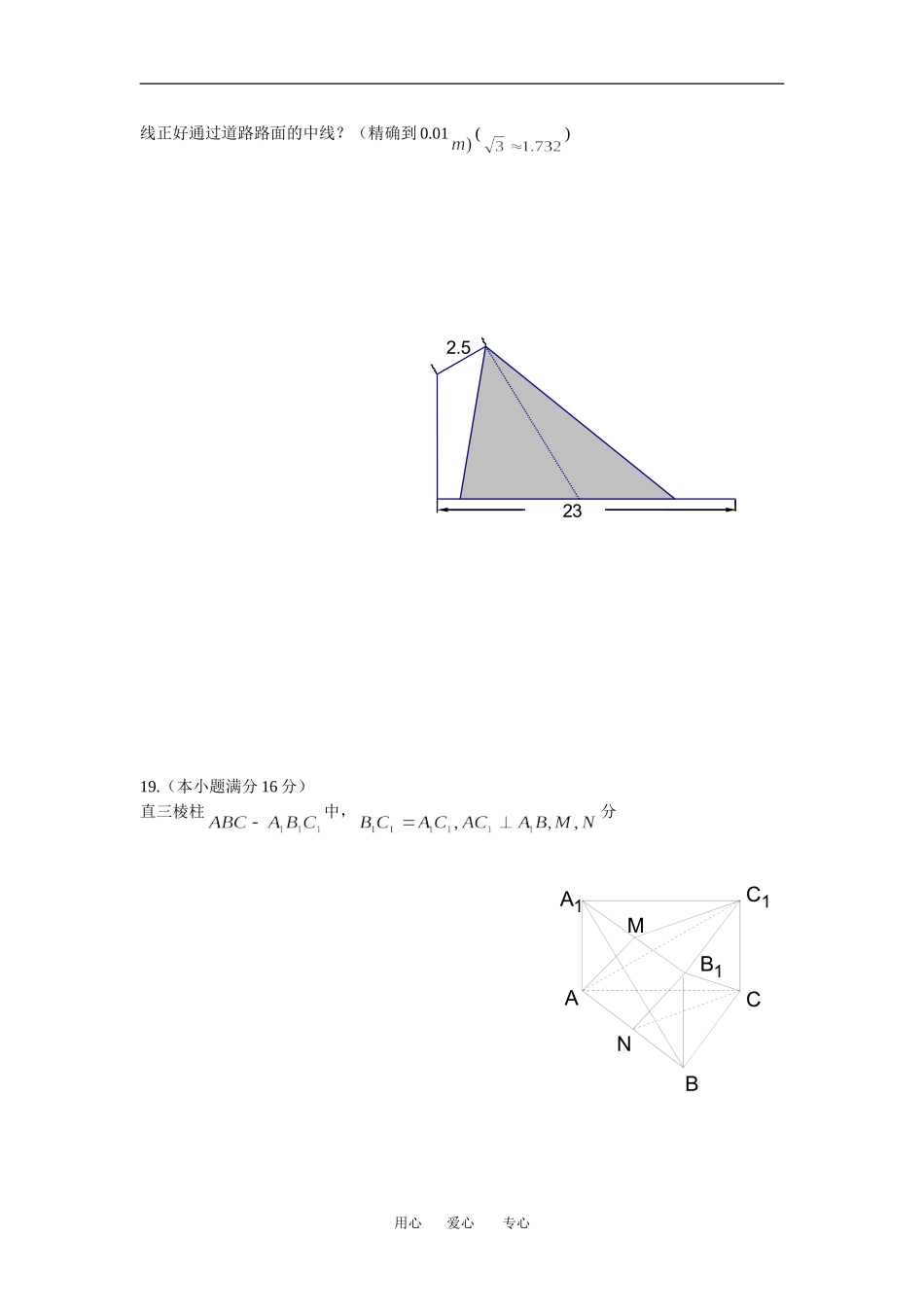
江苏省运河中学高二年级数学学科阶段性检测试卷考试时间为120分钟,试卷满分160分.一、填空题:(本大题共14小题,每小题5分,共70分)1.已知直线经过第二、三、四象限,则满足的条件是.2.已知直线(,则直线一定通过定点.3.已知直线与直线平行,则实数的值为.4.某商品的市场需求量万件)、市场供应量万件)与市场价格(元/件)分别近似地满足下列关系:当时的市场价格称为市场平衡价格,此时的需求量称为平衡需求量.现对每件商品征税3元时新的平衡价格为元.5.已知两条直线和都过点则过两点的直线方程为.6.已知直线过点,且在两坐标轴上的截距相等,则的方程为.7.用长、宽分别是与的矩形硬纸卷成的圆柱的侧面,则该圆柱底面的半径为.8.已知平面外的一条直线上有两点到距离相等,则与的位置关系是.9.如图,在正方体中,二面角的正切值为.10.若直线的倾斜角为则的取值范围为.11.直线与直线互相垂直,则实数的值为.12.设、是异面直线,则(1)一定存在平面,使且∥;(2)一定存在平面,使且;(3)一定存在平面,使,到的距离相等;(4)一定存在无数对平面与,使,,且∥;上述4个命题中正确命题的序号为.13.一个几何体的三视图如图所示,该几何体的内接圆柱侧面积的最大值为.14.设和为不重合的两个平面,给出下列命题:用心爱心专心D1C1B1A1DBCA第9题图俯视图4主视图左视图44·第13题图ABCDEF①若则②若则③若则④若则.上面命题中,真命题的序号(写出所有真命题的序号)二.解答题(本大题共有6小题,要求写出必要的过程)15.(本小题满分14分)已知直线(1)当为何值时,直线倾斜角为?(2)当为何值时,直线与轴平行?(3)当为何值时,直线与直线垂直?(4)当为何值时,直线与直线平行?16.(本小题满分14分)如图,在四面体中,,点分别是的中点.求证:(1)直线面;(2)平面面.17.(本小满分14分)、在长方体中,底面是边长为的正方体,侧棱长为分别是的中点,求证:平面平面18.(本小题满分16分)在路边安装路灯,路宽,灯杆长,且与灯柱成角.路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高为多少米时,灯罩轴用心爱心专心FEC1D1B1A1DCBA线正好通过道路路面的中线?(精确到0.01()19.(本小题满分16分)直三棱柱中,分用心爱心专心NMC1B1A1CBA232.520.(本小题满分16分)如图所示,已知直线与轴的正半轴分别交于两点,直线和分别交于且平分△的面积,求的最小值.高二年级数学学科阶段性检测试卷数学答题纸一、填空题(本大题共14小题,每小题5分,共70分.把答案填在下列相应的横线上,否则答题无效.)1.2.3.4.5.6.7.8.9.10.11.12.13._14.二、解答题(本大题共6小题,共90分.请把解答写在下面规定的答题框内,否则答题无效.用心爱心专心ACDBxyO姓名考试号班级…………………………………………密…………………………………………封…………………………线…………………………ABCDEF解答应写出必要的文字说明、证明过程或演算步骤.)15.(本题共14分)16.(本题共14分)17.(本题共15分)用心爱心专心18.(本题共15分)19.(本题共16分)用心爱心专心…………………………………………密…………………………………………封…………………………线………………………………FEC1D1B1A1DCBA232.5NMC1B1A1CBA20.(本题共16分)用心爱心专心ACDBxyO参考答案一、填空题1.2.3.14325.6或7或8.平行或相交.910.11.或12.(1)(3)13.14.(1)(2)二、解答题15.解:(1)(2)(3)(4)16.证明:(1) E,F分别是的中点.∴EF是△ABD的中位线,∴EF∥AD, EF∥面ACD,AD面ACD,∴直线EF∥面ACD;(2) AD⊥BD,EF∥AD,∴EF⊥BD, CB=CD,F是BD的中点,∴CF⊥BD又EF∩CF=F,∴BD⊥面EFC, BD面BCD,∴面面用心爱心专心17.证明: 分别是的中点,∴ 为的中点,∴故故中, ∴从而又为与的交点,∴是直角三角形,即∴平面又平面∴平面平面18.解:如图,记灯柱顶端为,灯罩顶为,灯杆为AB,灯罩轴线与道路中线交于C.以灯柱底端O点为原点,灯柱OB为y轴,建立如图所示的直角坐标系.点B的坐标为,点C的坐标为.因为,所以直线的倾斜角为则点A的坐标为即因为所以由点斜式,得直...