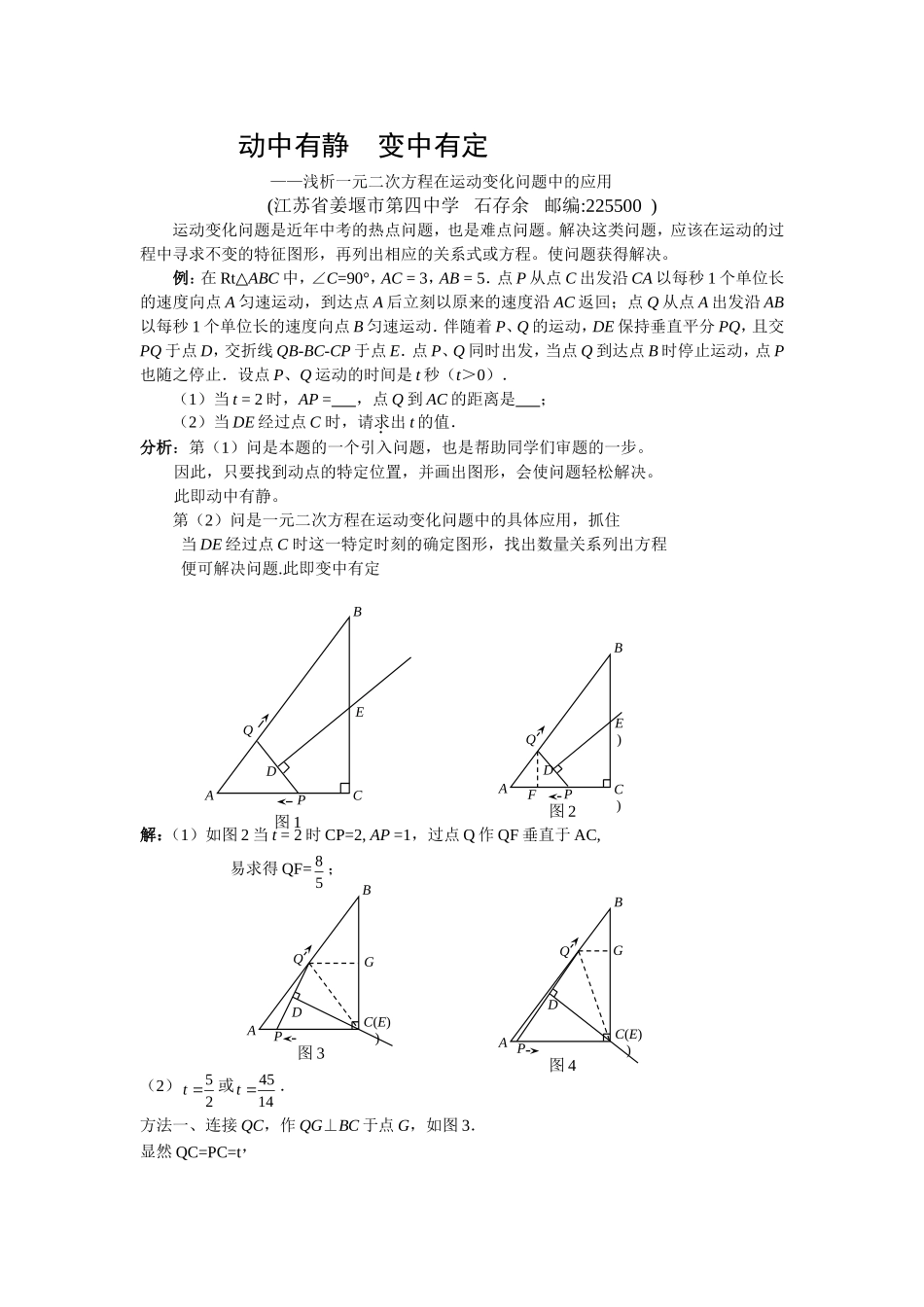
动中有静变中有定——浅析一元二次方程在运动变化问题中的应用(江苏省姜堰市第四中学石存余邮编:225500)运动变化问题是近年中考的热点问题,也是难点问题。解决这类问题,应该在运动的过程中寻求不变的特征图形,再列出相应的关系式或方程。使问题获得解决。例:在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当t=2时,AP=,点Q到AC的距离是;(2)当DE经过点C时,请求出t的值.分析:第(1)问是本题的一个引入问题,也是帮助同学们审题的一步。因此,只要找到动点的特定位置,并画出图形,会使问题轻松解决。此即动中有静。第(2)问是一元二次方程在运动变化问题中的具体应用,抓住当DE经过点C时这一特定时刻的确定图形,找出数量关系列出方程便可解决问题.此即变中有定解:(1)如图2当t=2时CP=2,AP=1,过点Q作QF垂直于AC,易求得QF=85;(2)52t或4514t.方法一、连接QC,作QG⊥BC于点G,如图3.显然QC=PC=t,ACBPQED图1AC)BPQD图2E)FAC(E))BPQD图3GAC(E))BPQD图4G222QCQGCG2234[(5)][4(5)]55tt.由22PCQC,得22234[(5)][4(5)]55ttt,解得52t.方法二、由CQCPAQ,得QACQCA,进而可得BBCQ,得CQBQ,∴52AQBQ.∴52t.②点P由A向C运动,DE经过点C,如图4.22234(6)[(5)][4(5)]55ttt,解得4514t∴52t或4514t点评:运动变化问题,除了动点以外,还有平移、旋转、轴对称等。其中关系错综复杂,但只要我们冷静分析,找准特征图形中的数量关系,再列出等式就能化繁为易。下面的问题相信同学们一定能自己解决!如图所示,四边形是矩形,,。动点P、Q分别同时从A、C出发,点P以3cm/s的速度向D移动,直到D为止,Q以2cm/s的速度向B移动。⑴P、Q两点从出发开始几秒后,四边形ABQP的面积是矩形面积的?何时四边形ABQP的面积最大,最大是多少?⑵P、Q从开始出发几秒后,?答案:⑴秒,当出发后,面积最大为64平方厘米⑵0.8秒