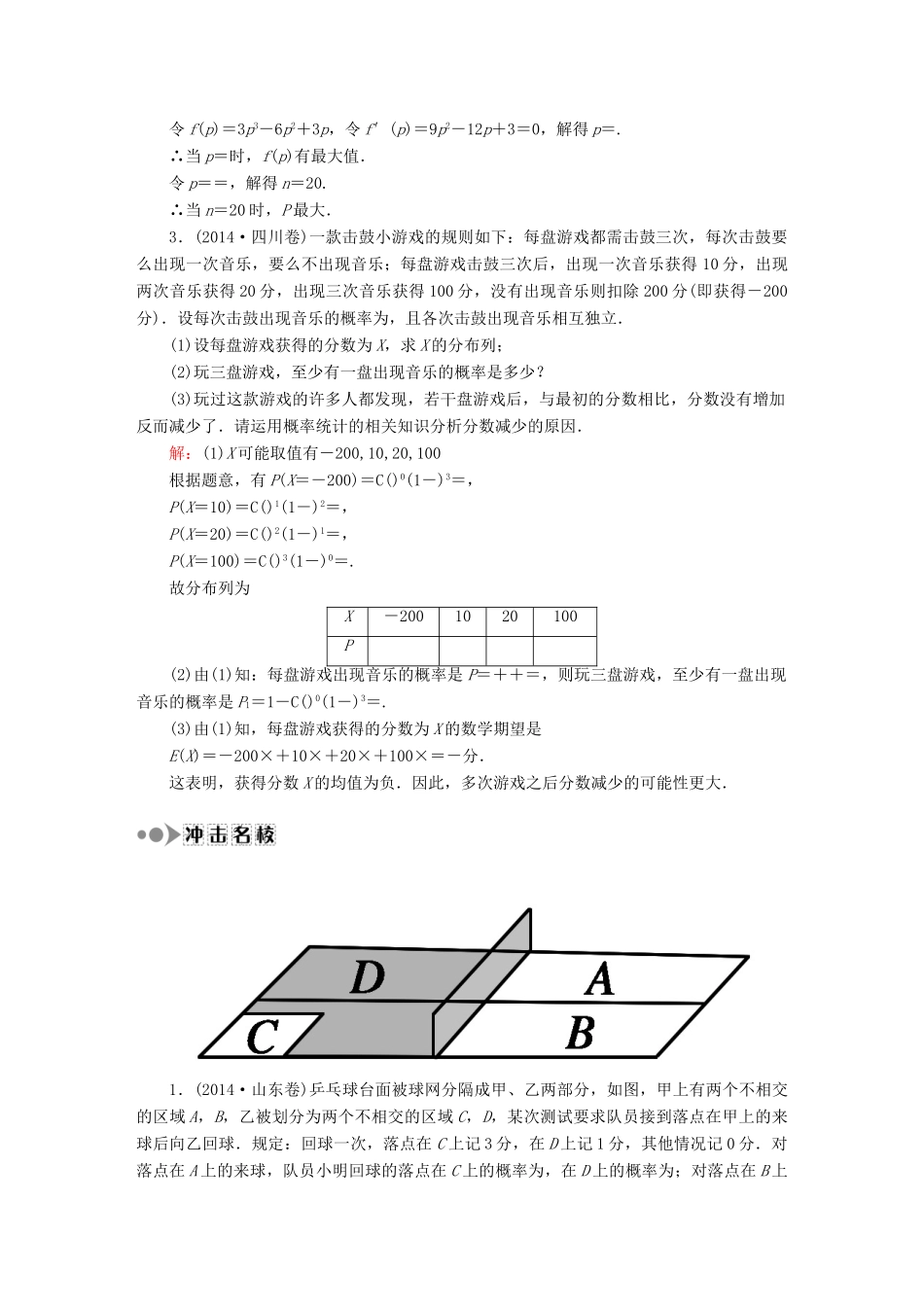
课时作业76高考中期望与方差的热点内容1.我国的高铁技术发展迅速,铁道部门计划在A、B两城市之间开通高速列车,假设列车在试运行期间,每天在8:00~9:00,9:00~10:00两个时间段内各发一趟由A城开往B城的列车(两车发车情况互不影响),A城发车时间及概率如下表所示:发车时间8:108:308:509:109:309:50概率若甲、乙两位旅客打算从A城到B城,他们到达A城火车站的时间分别是周六8:00和周日8:20.(只考虑候车时间,不考虑其他因素)(1)求甲、乙两人候车时间相等的概率;(2)设乙候车所需时间为随机变量ξ,求ξ的分布列和数学期望E(ξ).解:(1)由题意得,甲、乙两人的候车时间分别是10分钟,30分钟,50分钟的概率为P甲(10)=,P甲(30)=,P甲(50)=;P乙(10)=,P乙(30)=,P乙(50)=×=.所以甲、乙两人候车时间相等的概率P=×+×+×=.(2)ξ的所有可能取值为10,30,50,70,90(单位:分钟),所以ξ的分布列为ξ1030507090P数学期望E(ξ)=10×+30×+50×+70×+90×=.2.一个口袋装有n个红球(n≥5且n∈N)和5个白球,一次摸奖从中摸2个球(每次摸奖后放回),2个球颜色不同则为中奖.(1)试用n表示一次摸奖中奖的概率;(2)若n=5,求3次摸奖中奖次数ξ=1的概率及数学期望;(3)记3次摸奖恰有1次中奖的概率为P,当n取多少时,P最大?解:(1)记“一次从(n+5)个球中摸出2个球”为事件A,card(A)=.“一次从(n+5)个球中摸出2个球且2个球异色”为事件B,card(B)=5n,∴所求概率P=.(2)3次放回式摸奖中“每次从(n+5)个球中摸出2个球且2个球异色”为独立重复事件,当n=5时,获奖次数ξ~B,P(ξ=1)=,E(ξ)=3×=.(3)ξ~B(n,p),P(ξ=1)=Cp(1-p)2=3p3-6p2+3p,0