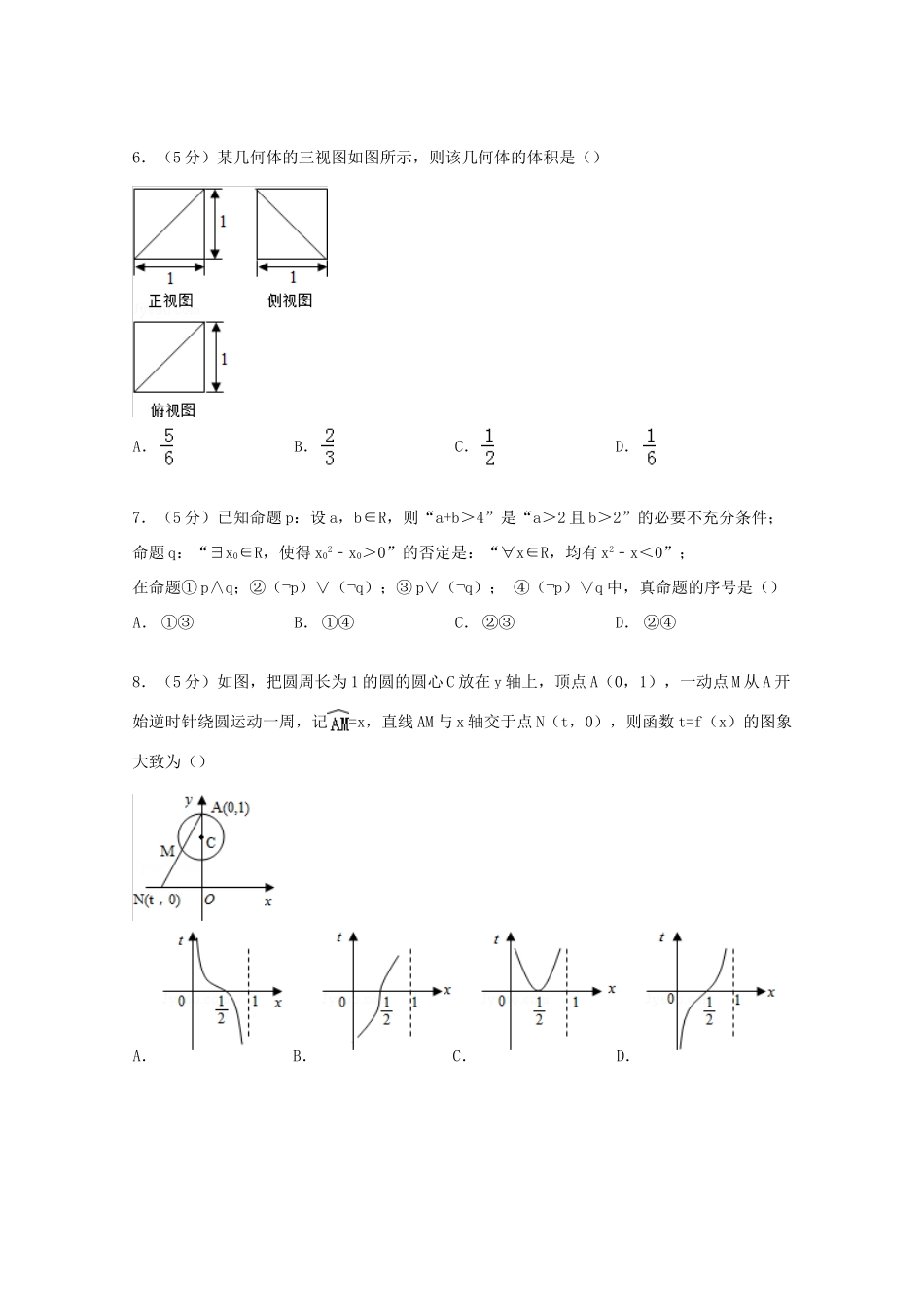
福建省厦门双十中学2015届高考数学热身试卷(理科)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.请把答案填涂在答题卷的相应位置.1.(5分)若cosθ=﹣,θ∈[0,π],则tanθ=()A.﹣2B.C.D.22.(5分)已知=2﹣i,则在复平面内,复数z对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)已知集合U=R,A={x|3x﹣x2>0},B={y|y=log2(x+1),x∈A},则A∩(∁UB)为()A.[2,3)B.(2,3)C.(0,2)D.∅4.(5分)已知三个正态分布密度函数(x∈R,i=1,2,3)的图象如图所示,则()A.μ1<μ2=μ3,σ1=σ2>σ3B.μ1>μ2=μ3,σ1=σ2<σ3C.μ1=μ2<μ3,σ1<σ2=σ3D.μ1<μ2=μ3,σ1=σ2<σ35.(5分)已知向量=(3,4),﹣2=(11,4),若向量与向量的夹角为θ,则cosθ=()A.B.﹣C.D.﹣6.(5分)某几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.7.(5分)已知命题p:设a,b∈R,则“a+b>4”是“a>2且b>2”的必要不充分条件;命题q:“∃x0∈R,使得x02﹣x0>0”的否定是:“∀x∈R,均有x2﹣x<0”;在命题①p∧q;②(¬p)∨(¬q);③p∨(¬q);④(¬p)∨q中,真命题的序号是()A.①③B.①④C.②③D.②④8.(5分)如图,把圆周长为1的圆的圆心C放在y轴上,顶点A(0,1),一动点M从A开始逆时针绕圆运动一周,记=x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为()A.B.C.D.9.(5分)设双曲线的右焦点为F(c,0),方程ax2+bx﹣c=0的两实根分别为x1,x2,则P(x1,x2)()A.必在圆x2+y2=2内B.必在圆x2+y2=2外C.必在圆x2+y2=2上D.以上三种情况都有可能10.(5分)某班试用电子投票系统选举班干部候选人.全班k名同学都有选举权和被选举权,他们的编号分别为1,2,…,k,规定:同意按“1”,不同意(含弃权)按“0”,令其中i=1,2,…,k,且j=1,2,…,k,则同时同意第1,2号同学当选的人数为()A.a11+a12+…+a1k+a21+a22+…+a2kB.a11+a21+…+ak1+a12+a22+…+ak2C.a11a12+a21a22+…+ak1ak2D.a11a21+a12a22+…+a1ka2k二、填空题:本大题共5小题,每小题4分,共20分.请把答案填在答题卷的相应位置.11.(4分)已知实数x,y满足不等式组,则x+2y的最大值为.12.(4分)某程序框图如图所示,该程序运行后输出的k的值是.13.(4分)若f(x)=cosx+3dx,则=.14.(4分)已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则二项式展开式中的常数项为.15.(4分)已知(2x+1)n=a0+a1x+a2x2+…+anxn,令x=0就可以求出常数,即a0=1,请研究其中蕴含的解题方法并完成下列问题:若ex=aixi,即ex=a0+a1x+a2x2+a3x3+a4x4+…+anxn+…,则+++…+=.三、解答题:本大题共5小题,每小题分数见旁注,共80分.解答应写出文字说明,证明过程或演算步骤.请在答题卷相应题目的答题区域内作答.16.(13分)已知直线两直线l1:xcosα+y﹣1=0;l2:y=xsin(α+),△ABC中,内角A,B,C对边分别为a,b,c,a=2,c=4,且当α=A时,两直线恰好相互垂直;(Ⅰ)求A值;(Ⅱ)求b和△ABC的面积.17.(13分)甲、乙两人为了响应政府“节能减排”的号召,决定各购置一辆纯电动汽车.经了解目前市场上销售的主流纯电动汽车,按续驶里程数R(单位:公里)可分为三类车型,A:80≤R<150,B:150≤R<250,C:R≥250.甲从A,B,C三类车型中挑选,乙从B,C两类车型中挑选,甲、乙二人选择各类车型的概率如下表:车型概率人ABC甲pq乙/若甲、乙都选C类车型的概率为.(Ⅰ)求p,q的值;(Ⅱ)求甲、乙选择不同车型的概率;(Ⅲ)某市对购买纯电动汽车进行补贴,补贴标准如下表:车型ABC补贴金额(万元/辆)345记甲、乙两人购车所获得的财政补贴和为X,求X的分布列.18.(13分)如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).(Ⅰ)若动点Q满足•+||=0,求点Q的轨迹C的方程;(Ⅱ)设椭圆Γ的中心在原点,对称轴在坐标轴上,直线l:y=kx+t(k≠0,t≠0)与轨迹C交...