1.1.1正弦定理-(2)VIP免费

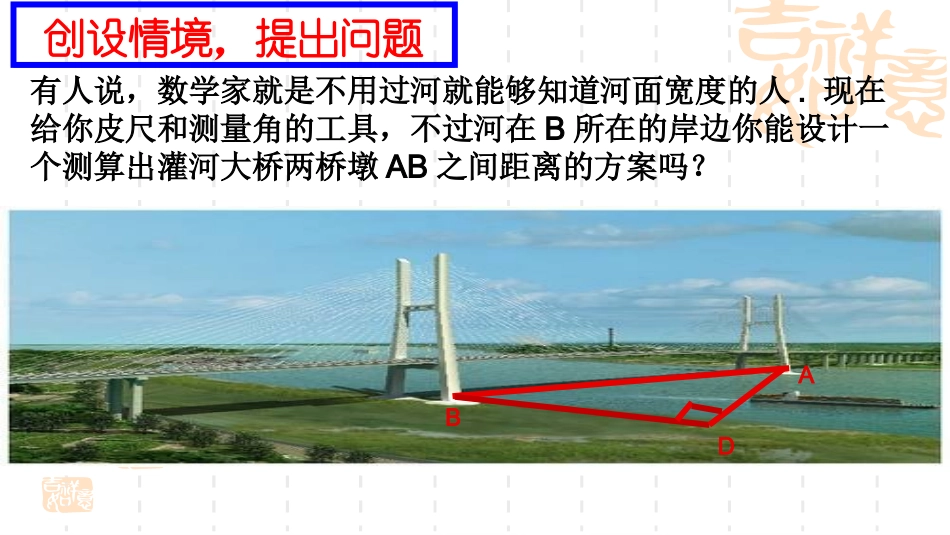
正弦定理江苏省滨海中学中学一级教师沈阳必修五模块问题情境ABD创设情境，提出问题有人说，数学家就是不用过河就能够知道河面宽度的人.现在给你皮尺和测量角的工具，不过河在B所在的岸边你能设计一个测算出灌河大桥两桥墩AB之间距离的方案吗？ABC创设情境，提出问题假如受到地理环境的制约，没法选择直角的测量点，你还能测算AB间的距离吗？ABC如何进一步研究三角形中边和角的关系呢？你能将你调整后的方案抽象为数学问题吗？00900,75,45,.BCBCAB已知求长在直角三角形中：sinsinsinabcABCcoscosbaABABCcba问：这两组关系对于正三角形成立吗？学生活动探究：直角三角形中边和角有什么样的关系?此时你有什么想法？对任意的三角形ABC，都有sinsinsinabcABC猜想1：coscosbaAB猜想2：观察特例，提出猜想数学实验，深入探究对任意的三角形ABC，都有sinsinsinabcABC归纳总结，完善猜想从最直观的几何层面思考如图:作AB上的高是CD，则有sinsinbcBCsinsinsinabcABCsin,sinCDaBCDbAsinsinaBbA所以sinsinabAB得到DACBbac同理有：设最大角为锐角时AsinsinCDCDABba证明猜想，得出结论问：以上等式是否仍然成立?DBACbca学生活动当为钝角时AsinCDBasinsin()sinCABCADCDCADbsin,sinCDaBCDbA下证同上sinsinsinabcABCDBACabc从向量分析层面思考问题1：从向量角度来看，任何一个三角形可以看作由首尾相接的三个向量构成，这三个向量之和等于什么？问题2：如何将这个向量关系转化为数量关系？0或ABBCCAABCBCA��ABCBCA�向量式数量式数量积点乘向量_____()______辅助向量ABCBCA�问题3：如何选取辅助向量呢？DBACbca_____()______辅助向量ABCBCA�BACabcDCD�CD�0CBCDCACD�0coscos22aCDBbCDA�sin=sinsinsinabaBbAAB即有：sinsinbcBC同理可证：sinsinsinabcABC设最大角为锐角时A设最大角为钝角时A0coscos22aCDBbCDA�正弦定理三角形的各边和它所对角的正弦之比相等，即CcBbAasinsinsin表达：简洁美结构：对称美内在：和谐美注：正弦定理是对三角形大边对大角定理的定量刻画例1、在前面的测量问题中，如何计算两桥墩之间的距离？数学应用A075045BC900060.sinsin29002300632BCCABA解：在ABC中，A=由正弦定理得：例2、045103106aABCB在中，已知A，b，求课堂总结1.你能小结一下本节课探究正弦定理的思路吗？发现问题数学证明1、化斜为直，构造直角三角形2、构造向量的数量积（向量法）3.运用正弦定理可以解决什么问题？提出猜想实验检验2.证明正弦定理时采用了哪些方法运用正弦定理可以解决下列两类解斜三角形问题：（1）已知两角与任一边，求其他两边和一角，此时解是唯一的；（2）已知两边和其中一边的对角，求另一边的对角，此时解不一定唯一。课后探究sinsinsinabcKABC是三角形的怎样一个几何量？如何证明？结束语：通过本节的学习，我们对三角形的性质从定性刻画走向定量刻画，实现了对三角形认识质的飞跃.我们发现看似十分简单的三角形背后隐含着十分深刻的数学结论，并且这些数学结论可以用简洁、对称、和谐、优美的数学公式表示.在探究正弦定理的过程中，我们强烈的感受到数学思维的力量和人类心智的伟大.