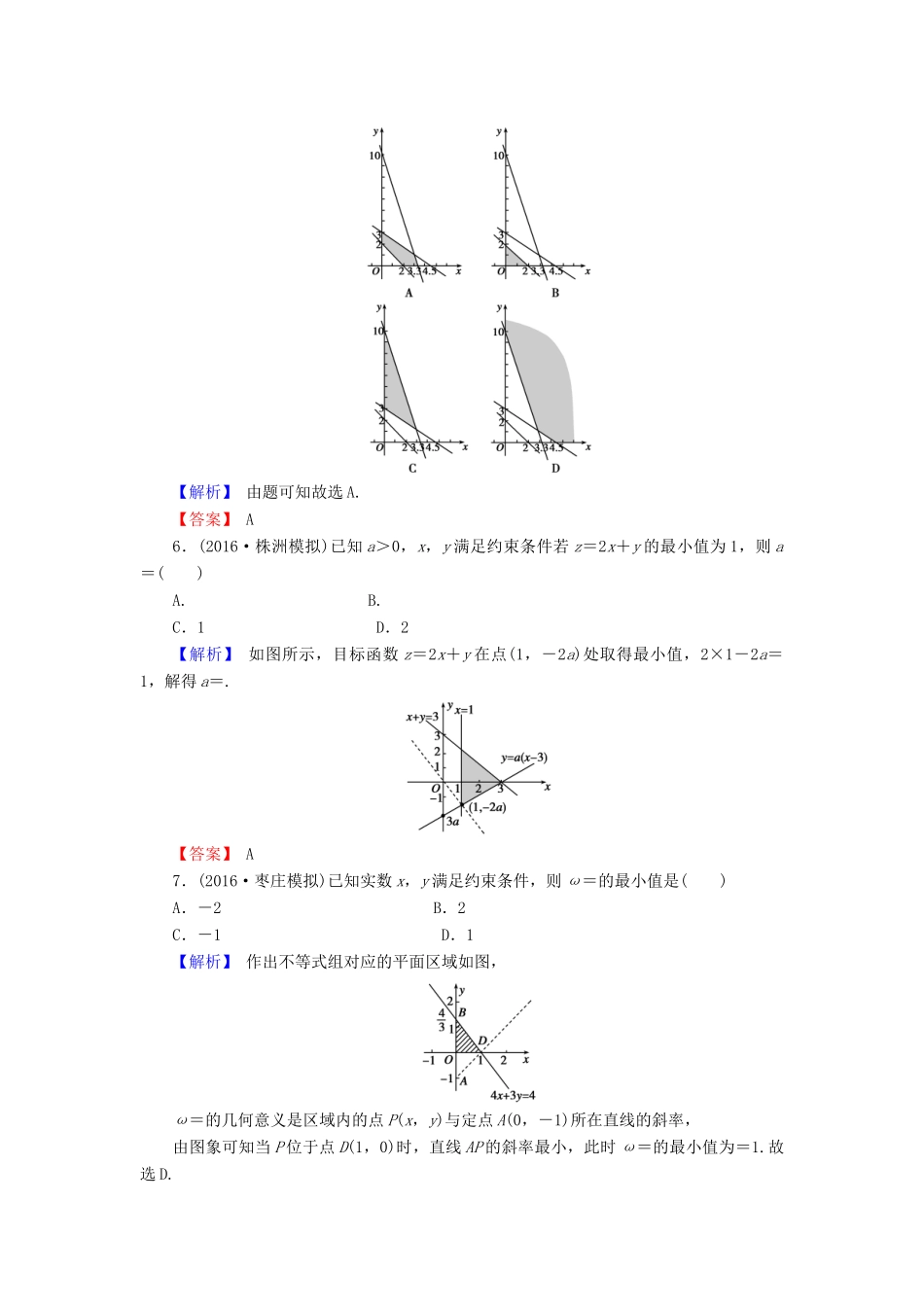
7.3二元一次不等式(组)与简单的线性规划问题A组专项基础训练(时间:25分钟)1.直线2x+y-10=0与不等式组表示的平面区域的公共点有()A.0个B.1个C.2个D.无数个【解析】由不等式组画出平面区域如图(阴影部分).直线2x+y-10=0恰过点A(5,0),且其斜率k=-2<kAB=-,即直线2x+y-10=0与平面区域仅有一个公共点A(5,0).【答案】B2.(2015·天津)设变量x,y满足约束条件则目标函数z=x+6y的最大值为()A.3B.4C.18D.40【解析】画出约束条件的可行域如图阴影部分,作直线l:x+6y=0,平移直线l可知,直线l过点A时,目标函数z=x+6y取得最大值,易得A(0,3),所以zmax=0+6×3=18,选C.【答案】C3.(2017·湖北荆州二模)已知x,y满足约束条件则z=2x+y的最大值为()A.3B.-3C.1D.【解析】作出可行域,如图所示的阴影部分,当直线z=2x+y过点A(2,-1)时,z最大,是3,故选A.【答案】A4.(2016·河南洛阳期中)若实数x,y满足不等式组且x+y的最大值为9,则实数m=()A.-2B.-1C.1D.2【解析】先根据约束条件画出可行域,如图.设z=x+y,则y=-x+z,将z转化为直线y=-x+z在y轴上的截距.当直线z=x+y经过直线x-my+1=0与直线2x-y-3=0的交点A时,z最大.由得A(4,5),将点A的坐标代入x-my+1=0得m=1,故选C.【答案】C5.(2016·北京丰台模拟)某工厂生产甲、乙两种产品,已知生产每吨甲种产品要用A原料3吨,B原料2吨;生产每吨乙种产品要用A原料1吨,B原料3吨.该工厂每天生产甲、乙两种产品的总量不少于2吨,且每天消耗的A原料不能超过10吨,B原料不能超过9吨.如果设每天甲种产品的产量为x吨,乙种产品的产量为y吨,则在坐标系xOy中,满足上述条件的x,y的可行域用阴影部分表示正确的是()【解析】由题可知故选A.【答案】A6.(2016·株洲模拟)已知a>0,x,y满足约束条件若z=2x+y的最小值为1,则a=()A.B.C.1D.2【解析】如图所示,目标函数z=2x+y在点(1,-2a)处取得最小值,2×1-2a=1,解得a=.【答案】A7.(2016·枣庄模拟)已知实数x,y满足约束条件,则ω=的最小值是()A.-2B.2C.-1D.1【解析】作出不等式组对应的平面区域如图,ω=的几何意义是区域内的点P(x,y)与定点A(0,-1)所在直线的斜率,由图象可知当P位于点D(1,0)时,直线AP的斜率最小,此时ω=的最小值为=1.故选D.【答案】D8.(2016·贵阳模拟)已知实数x,y满足则z=2x-2y-1的取值范围是()A.B.[0,5]C.D.【解析】画出不等式组所表示的区域,如图中阴影部分所示,可知2×-2×-1≤z<2×2-2×(-1)-1,即z的取值范围是.【答案】D9.(2016·山西质检)若变量x,y满足则2x+y的取值范围为________.【解析】作出满足不等式组的平面区域,如图中阴影部分所示,平移直线2x+y=0,经过点(1,0)时,2x+y取得最大值2×1+0=2,经过点(-1,0)时,2x+y取得最小值2×(-1)+0=-2,所以2x+y的取值范围为[-2,2].【答案】[-2,2]10.(2016·天津卷)某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:原料肥料ABC甲483乙5510现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y表示计划生产甲、乙两种肥料的车皮数.(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;(2)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.【解析】(1)由已知,x,y满足的数学关系式为该二元一次不等式组所表示的平面区域为图1中的阴影部分.(2)设利润为z万元,则目标函数为z=2x+3y.考虑z=2x+3y,将它变形为y=-x+,这是斜率为-,随z变化的一族平行直线.为直线在y轴上的截距,当取最大值时,z的值最大.又因为x,y满足约束条件,所以由图2可知,当直线z=2x+3y经过可行域上的点M时,截距最大,即z最大.解方程组得点M的坐标为(20,24).所以zmax=2×20+3×24=112.答:生产甲种肥料20车皮、乙种肥料24车皮时利润最大,...