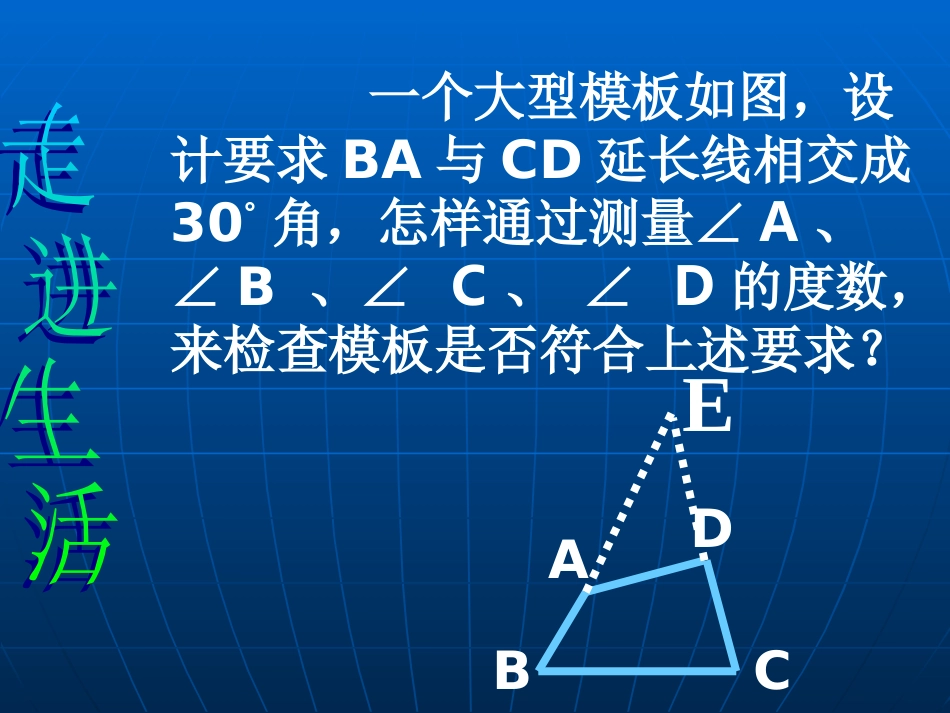
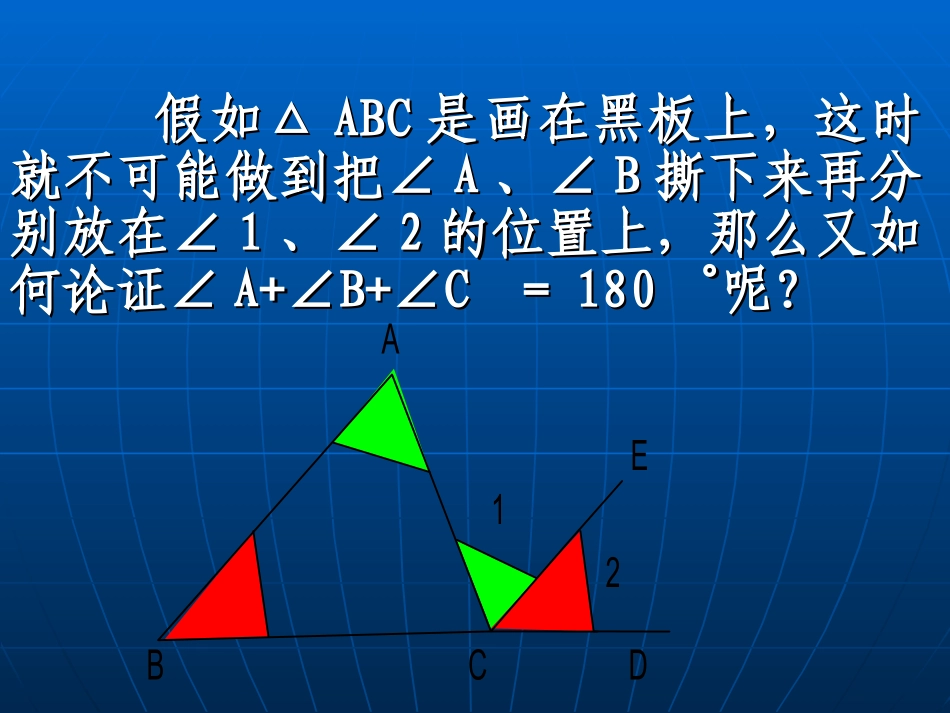
6.56.5三角形内角和三角形内角和定理的定理的证明证明榆林市第七中学导学者:符洁北师大版八年级下册一个大型模板如图,设计要求BA与CD延长线相交成30°角,怎样通过测量∠A、∠B、∠C、∠D的度数,来检查模板是否符合上述要求?BACDE假如△假如△ABCABC是画在黑板上,这时是画在黑板上,这时就不可能做到把∠就不可能做到把∠AA、∠、∠BB撕下来再分撕下来再分别放在∠别放在∠11、∠、∠22的位置上,那么又如的位置上,那么又如何论证∠何论证∠A+∠B+∠C=180A+∠B+∠C=180呢?゜呢?゜ABC12DE三角形的三个内角之和等于三角形的三个内角之和等于180180゜゜分析:可延长BC到D,过点C作射线CE∥AB,得∠1、∠2,由CE∥AB,可得∠A=∠1,∠B=∠2,这样就相当于把∠A移到了∠1的位置,∠B移到了∠2的位置。BACDE12证明:三角形内角和定理已知:△已知:△ABCABC求证:∠求证:∠A+∠B+∠C=180A+∠B+∠C=180゜゜探索三角形内角和定理探索三角形内角和定理的其他证明思路的其他证明思路你还有哪些证明方法可以达到同样的效果?添加不同的辅助线大家借助你们手中的三角形纸片拼一拼,想一想,画一画,看看谁的办法更多,更好。议一议:在证明三角形内角和定理时,有的同学的想法是把三个角“凑”到点A处,他过点A作直线PQBC∥。他的想法可行吗?你还有其他的证明方法吗?BACpQ上面的证明方法是通过平行线把上面的证明方法是通过平行线把∠∠AA、∠、∠BB、∠、∠CC““凑凑””到角的顶点处或三角形的边到角的顶点处或三角形的边上,如(图上,如(图11)、(图)、(图22),也可以把这三个角),也可以把这三个角““凑凑””在别的位置上,如(图在别的位置上,如(图33)、(图)、(图44))..几种常见的拼凑思路321FEDCBAECBA(1)(2)TSNABCPQRMTSNABCPQRM(3)(4)把三个角“凑”到三角形内一点如(图3),“凑”到三角形外一点如(图4)1、直角三角形的两锐角之和是多少度?等边三角形的每一个内角是多少度?请说明你的理由。三角形内角和定理的应用ABC推论:直角三角形的两个锐角互余;等边三角形的每个内角是60°ABC2、已知:如图在△ABC中,DE∥BC,∠A=60°,∠C=70°。则∠ADE的度数为DCBAE70°60°50°33、、如图,直线如图,直线AB∥CD,AB∥CD,在在ABAB、、CDCD外外有一点有一点PP,连结,连结PBPB、、PDPD,交,交CDCD于于EE点点..则∠则∠BB、∠、∠DD、、∠∠PP之间是否存在之间是否存在一定的关系?一定的关系?猜想:∠B=D+P∠∠ABCPDE124、如图,∠ABC与∠ACB的角平分线交于点O,求证:∠BOC=900+-∠ABACO1221课堂小结1、本节知识要点:(1)三角形内角和定理:三角形三个内角的和等于180°(2)推论:直角三角形的两个锐角互余。2、三角形内角和定理的证明的基本思路:(1)把三个内角拼在一起构成平角(2)利用“两直线平行,同旁内角互补”实现转化。(3)证明中为了把三个分散的角加在一起,需要添加辅助线,实质是通过平行线将分散的角集中为共顶点的角。3、本节课还有什么疑问?你想进一步探究的问题是什么?谈谈你的学习体会。谢谢指导SeeYou