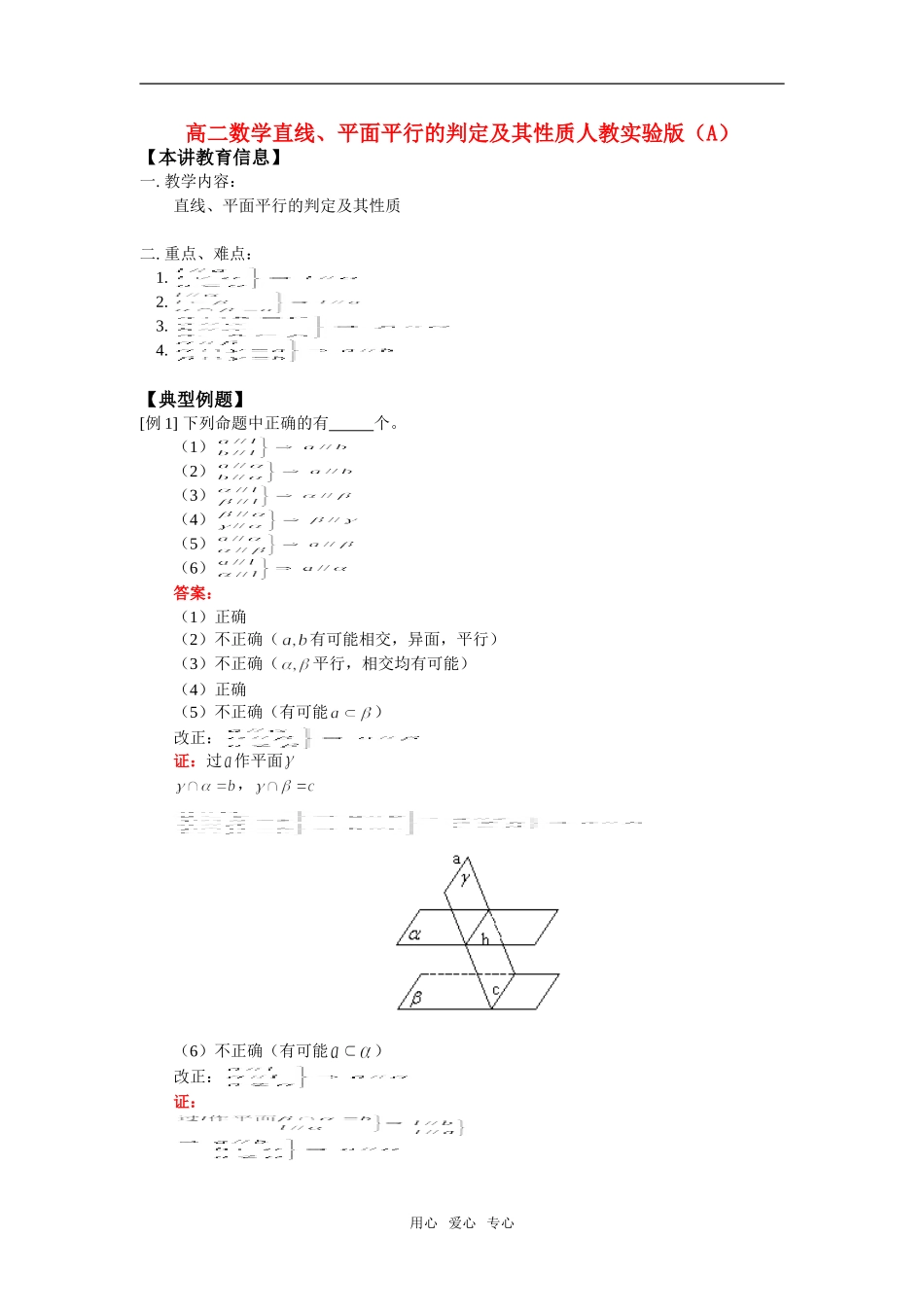
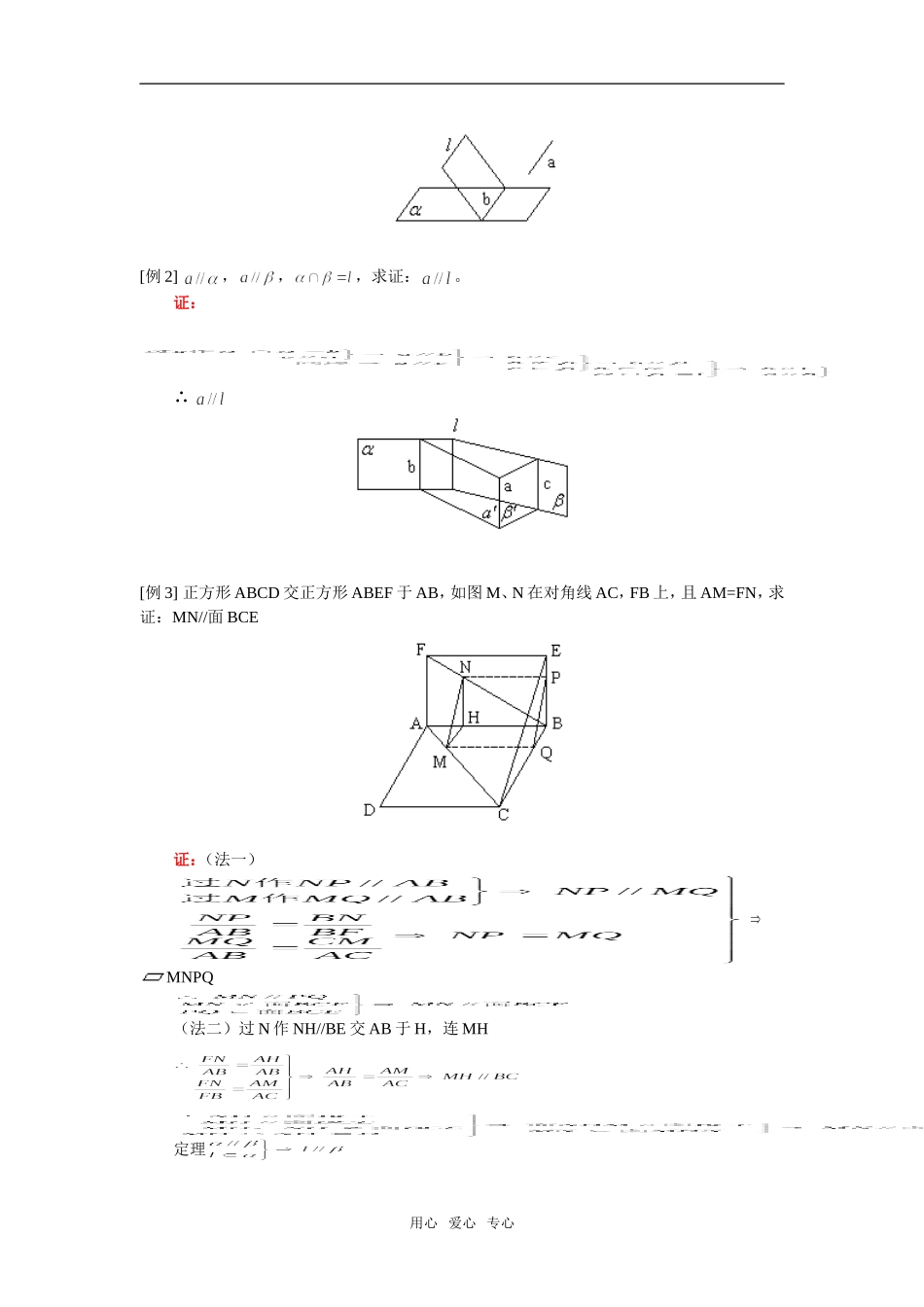
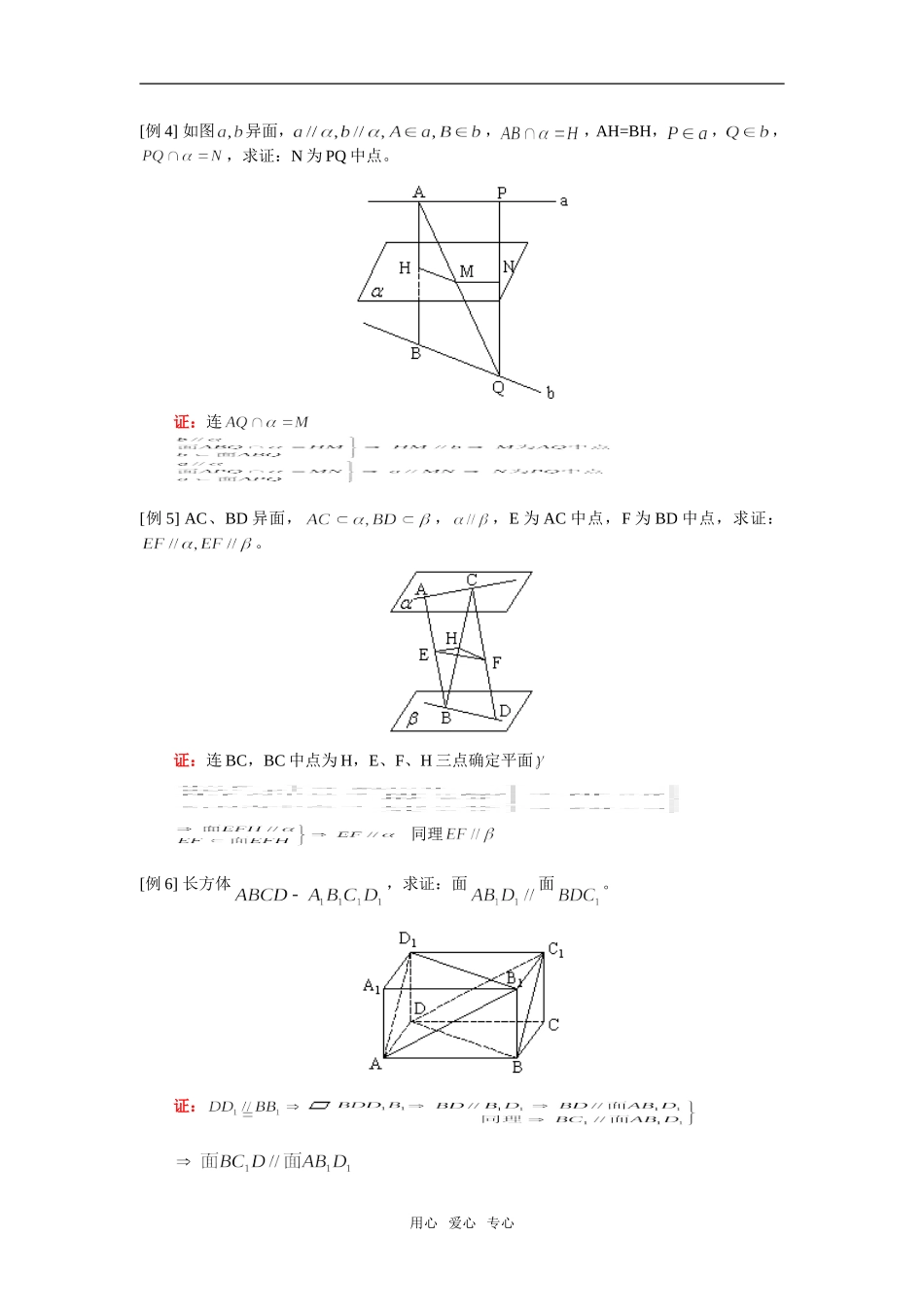
高二数学直线、平面平行的判定及其性质人教实验版(A)【本讲教育信息】一.教学内容:直线、平面平行的判定及其性质二.重点、难点:1.2.3.4.【典型例题】[例1]下列命题中正确的有个。(1)(2)(3)(4)(5)(6)答案:(1)正确(2)不正确(有可能相交,异面,平行)(3)不正确(平行,相交均有可能)(4)正确(5)不正确(有可能)改正:证:过作平面,(6)不正确(有可能)改正:证:用心爱心专心[例2],,,求证:。证:∴[例3]正方形ABCD交正方形ABEF于AB,如图M、N在对角线AC,FB上,且AM=FN,求证:MN//面BCE证:(法一)MNPQ(法二)过N作NH//BE交AB于H,连MH定理用心爱心专心[例4]如图异面,,,AH=BH,,,,求证:N为PQ中点。证:连[例5]AC、BD异面,,,E为AC中点,F为BD中点,求证:。证:连BC,BC中点为H,E、F、H三点确定平面同理[例6]长方体,求证:面面。证:用心爱心专心[例7]四棱锥中,底面为直角梯形,AD//BC,,PA=AD=,AB=BC=,E为PD中点,求证:CE//面PAB。证:F为PA中点[例8]长方体中E、F分别为、AC中点,求证:面。证:[例9]长方体,如图E、F、G、H、M、N为各棱中点,求证:E、F、G、H、M、N六点共面。用心爱心专心证:确定平面同理EF//NG,确定平面N、E、F三点不共线为的公共点过N、E、F三点的平面有且只有一个∴重合∴M、N、E、F、G五点共面同理E、F、M、N、G、H六点共面【模拟试题】(答题时间:20分钟)1.(1),过A作与平行的直线。(2),过A作与平行的直线。(3),过A作与平行的平面。(4),过A作与平行的平面。(5),过作与平行的平面有。(6)异面,过与平行的平面有。(7)异面,,过A与平行的平面有。(8)异面,,,过A作与均相交的直线。(9)均异面,空间与均相交的直线有。2.三棱柱,D为BC中点,求证:面。3.正四棱锥中,,在PB上是否存在一点F使AF//面BDE,若存在,求BF,若不存在说明理由。用心爱心专心4.异面,,与的位置关系。5.给出下列命题:①一个平面内有无数条直线平行于另一个平面,则②一个平面内两条不平行直线都平行于另一个平面,则③过平面外一点,且与平行的直线在同一个平面内④,,则其中正确命题的个数是()A.1个B.2个C.3个D.4个6.下列命题中正确的个数为()(1),,则(2),,则(3),,则(4),,则A.0B.1C.2D.3用心爱心专心试题答案1.(1)有且仅有1条(2)无数条(3)无数个(4)有且仅有一个(5)一个或不存在(6)有且仅有一个(7)一个或不存在(8)一个或不存在(9)无数条2.,连DE3.∴4.平行5.B6.A用心爱心专心