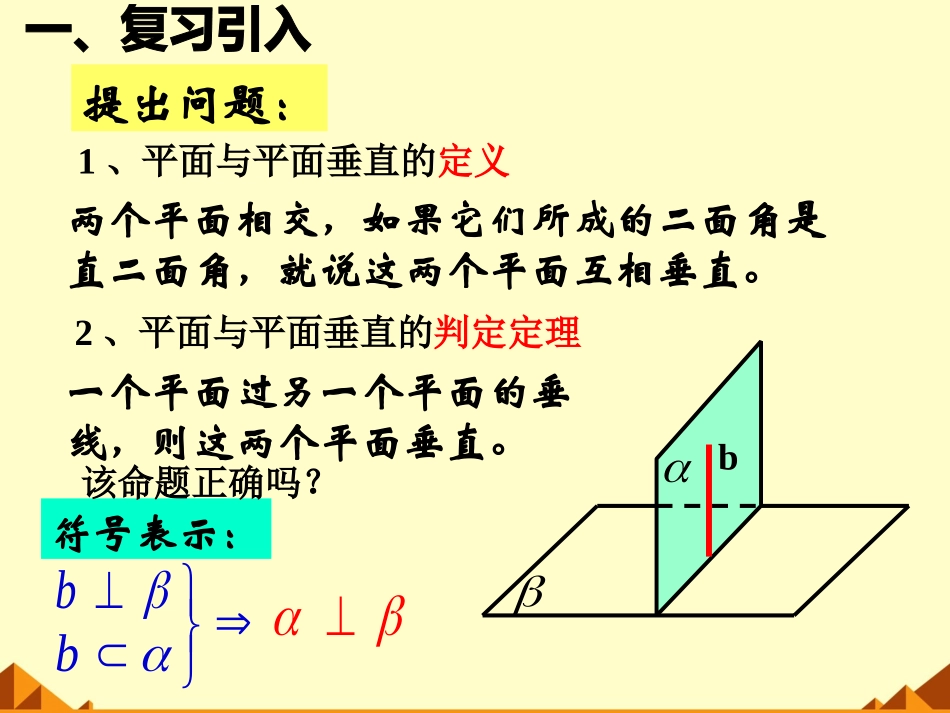
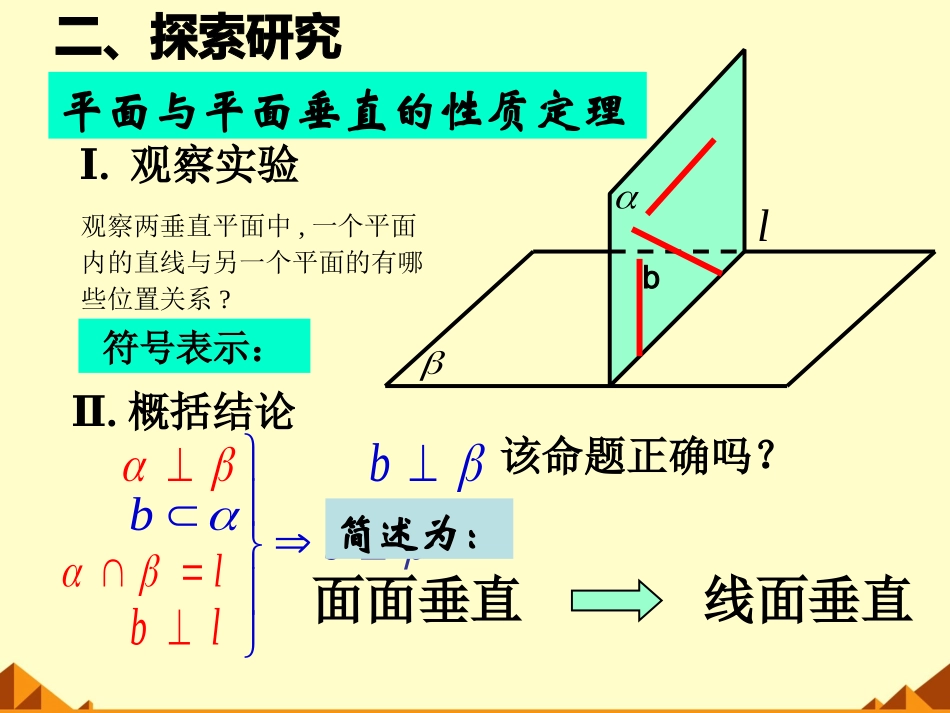
平面与平面垂直的性质1、平面与平面垂直的定义2、平面与平面垂直的判定定理一个平面过另一个平面的垂线,则这两个平面垂直。符号表示:b两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。bb提出问题:该命题正确吗?bⅠ.观察实验观察两垂直平面中,一个平面内的直线与另一个平面的有哪些位置关系?Ⅱ.概括结论lllb平面与平面垂直的性质定理bb简述为:面面垂直线面垂直b该命题正确吗?符号表示:Ⅲ.知识应用练习1:判断正误。已知平面α⊥平面β,α∩β=l下列命题(2)垂直于交线l的直线必垂直于平面β()(3)过平面α内任意一点作交线的垂线,则此垂线必垂直于平面β()(1)平面α内的任意一条直线必垂直于平面β()√××探究:已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线a与平面β的位置关系?巩固练习:下列命题中,正确的是()A、过平面外一点,可作无数条直线和这个平面垂直B、过一点有且仅有一个平面和一条定直线垂直C、若a,b异面,过a一定可作一个平面与b垂直D、a,b异面,过不在a,b上的点M,一定可以作一个平面和a,b都垂直.例1:如图,在长方体ABCD-A’B’C’D’中,(1)判断平面ACC’A’与平面ABCD的位置关系(2)MN在平面ACC’A’内,MNAC⊥于M,判断MN与AB的位置关系。ABCDA’B’C’D’MN例2:如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,BOPAC(2)判断平面PBC与平面PAC的位置关系。(1)判断BC与平面PAC的位置关系,并证明。(1)证明: AB是⊙O的直径,C是圆周上不同于A,B的任意一点∴∠ACB=90°BCAC∴⊥又 平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BC平面ABCBC∴⊥平面PAC(2)又 BC平面PBC,∴平面PBC⊥平面PAC解题反思2、本题充分地体现了面面垂直与线面垂直之间的相互转化关系。1、面面垂直的性质定理给我们提供了一种证明线面垂直的方法面面垂直线面垂直性质定理判定定理例垂直于同一平面的两平面的交线垂直于这个平面。已知:α⊥γ,β⊥γ,α∩β=а,求证:a⊥γ.证法一:γαβabcPMN设α∩γ=b,β∩γ=c,在γ内任取一点P,作PM⊥b于M,PN⊥C于N.因为α⊥γ,β⊥γ,所以PM⊥α,PN⊥β.因为α∩β=a,所以PM⊥a,PN⊥a,所以a⊥γ.线线垂直线面垂直γαβa已知:αγ⊥,βγ,α∩β=а,⊥求证:aγ.⊥证法二:Pb任取Pa∈,过点P作b⊥γ.∩∩因为α⊥γ,所以bα,因为β⊥γ,因此bβ,故α∩β=b.由已知α∩β=a,所以a与b重合,所以a⊥γ.同一法γαβa已知:αγ⊥,βγ,α∩β=⊥а,求证:aγ.⊥证法三:bcb′c′设αγ⊥于b,βγ⊥于c.在α内作b′⊥b,所以b′γ.⊥同理在β内作c′⊥c,有c′⊥γ,所以b′‖c′,∩∩∩又b′β,c′β,所以b′‖β.又b′α,α∩β=a,所以b′‖a,故aγ.⊥线线平行线面垂直练习1:如图,已知PA⊥平面ABC,平面PAB⊥平面PBC,求证:BC⊥平面PABPABCE证明:过点A作AEPB⊥,垂足为E, 平面PAB⊥平面PBC,平面PAB∩平面PBC=PB,∴AE⊥平面PBC BC平面PBCAEBC∴⊥ PA⊥平面ABC,BC平面ABC∴PABC⊥ PA∩AE=A,∴BC⊥平面PAB练习2:如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,求BD与平面ABC所成的角。ABCDDABCOO折成1、平面与平面垂直的性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。2、证明线面垂直的两种方法:线线垂直→线面垂直;面面垂直→线面垂直3、线线、线面、面面之间的关系的转化是解决空间图形问题的重要思想方法。1、如图,α⊥β,α∩β=l,ABα,AB⊥l,BCβ,DEβ,BC⊥DE.求证:AC⊥DE.ABCDEl2.如图,平面AED⊥平面ABCD,△AED是等边三角形,四边形ABCD是矩形,(1)求证:EACD⊥MDECAB(2)若AD=1,AB=,求EC与平面ABCD所成的角。2小结线线垂直线面垂直面面垂直αβaAB线线平行面面平行平面与平面垂直的性质定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.符号表示:blllbbb简述为:面面垂直线面垂直AA1B1C1BCE思考题:...