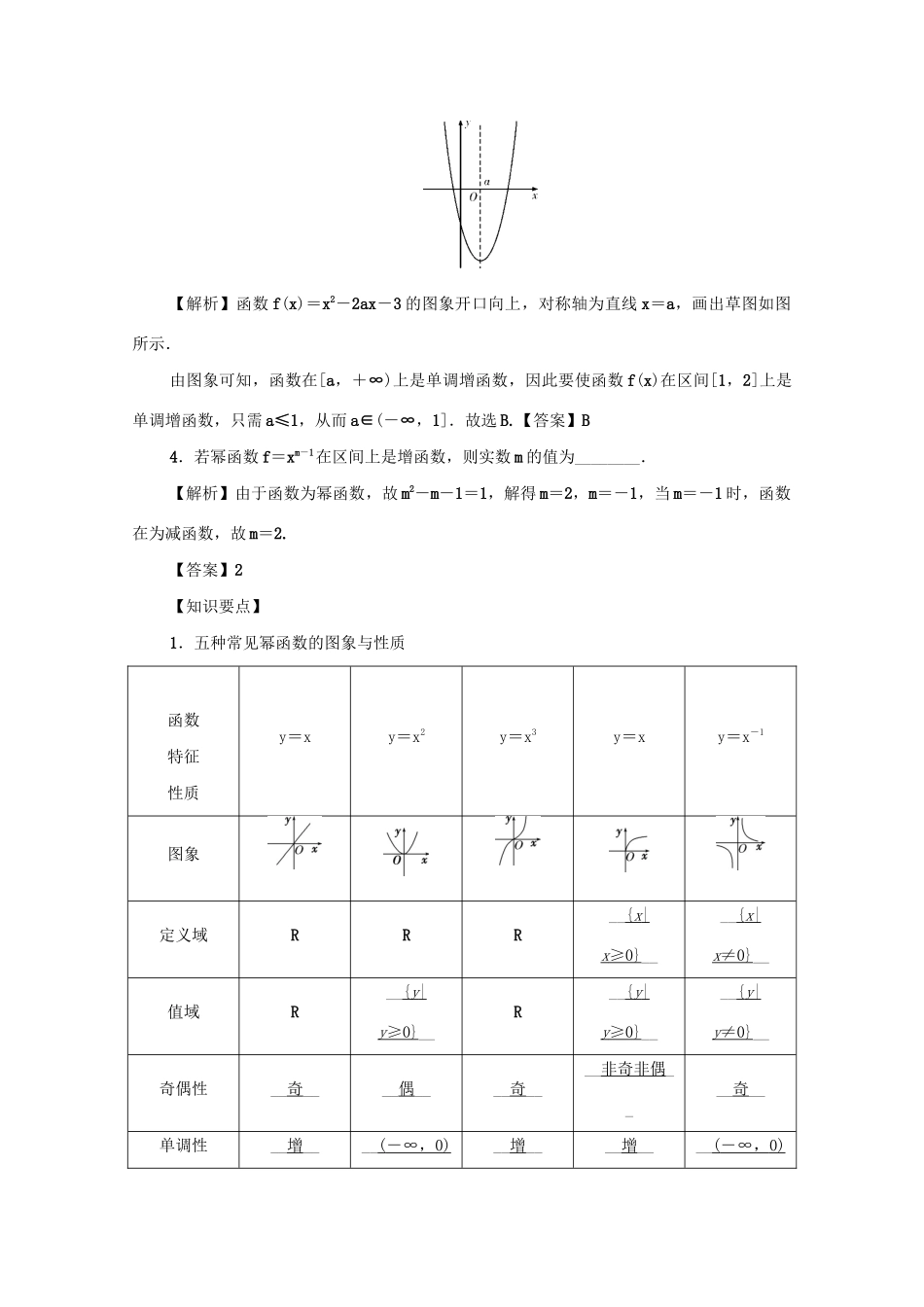
第9讲二次函数与幂函数夯实基础【p22】【学习目标】1.熟练掌握二次函数的概念、图象、性质及其与一元二次方程、一元二次不等式的联系.2.了解幂函数的概念,结合函数y=x,y=x2,y=x3,y=,y=x的图象了解它们的变化情况.【基础检测】1.函数y=-+2的顶点坐标是()A.(1,2)B.(1,-2)C.(-1,2)D.(-1,-2)【解析】 y=-+2=-+2,∴顶点坐标是(-1,2).【答案】C2.幂函数y=f(x)的图象经过点(2,4),则该幂函数的解析式为()A.y=2xB.y=x2C.y=x+2D.y=2x【解析】设f(x)=xα, 其图象过点(2,4),∴2α=4,α=2,即f(x)=x2.故选B.【答案】B3.已知函数f=x2-2ax-3在区间上是单调增函数,则实数a的取值范围为()A.B.C.D.【解析】函数f(x)=x2-2ax-3的图象开口向上,对称轴为直线x=a,画出草图如图所示.由图象可知,函数在[a,+∞)上是单调增函数,因此要使函数f(x)在区间[1,2]上是单调增函数,只需a≤1,从而a∈(-∞,1].故选B.【答案】B4.若幂函数f=xm-1在区间上是增函数,则实数m的值为________.【解析】由于函数为幂函数,故m2-m-1=1,解得m=2,m=-1,当m=-1时,函数在为减函数,故m=2.【答案】2【知识要点】1.五种常见幂函数的图象与性质函数特征性质y=xy=x2y=x3y=xy=x-1图象定义域RRR__{x|x≥0}____{x|x≠0}__值域R__{y|y≥0}__R__{y|y≥0}____{y|y≠0}__奇偶性__奇____偶____奇____非奇非偶____奇__单调性__增____(-∞,0)__增____增____(-∞,0)减,(0,+∞)增__和(0,+∞)减__公共点(1,1)2.二次函数解析式的三种形式(1)一般式:f(x)=__ax2+bx+c(a≠0)__;(2)顶点式:f(x)=__a(x-m)2+n(a≠0)__;(3)零点式:f(x)=__a(x-x1)(x-x2)(a≠0)__.3.二次函数的图象和性质f(x)=ax2+bx+ca>0a<0图象定义域x∈R值域单调性在上递减,在上递增在上递增,在上递减奇偶性b=0时为偶函数,b≠0时既不是奇函数也不是偶函数图象特点①对称轴:x=-;②顶点:典例剖析【p23】考点1幂函数的图象与性质(1)函数y=的图象是()【解析】函数y=可化为y=x3,当x=时,求得y=<,选项B,D不合题意,可排除选项B,D;当x=2时,求得y=8>2,选项A不合题意,可排除选项A,故选C.【答案】C(2)已知幂函数f(x)=xα的图象过点(4,2).若f(m)=3,则实数m的值为()A.B.±C.±9D.9【解析】依题意有2=4α,得α=,所以f(x)=x,当f(m)=m=3时,m=9.【答案】D(3)已知幂函数y=f(x)的图象经过点,且f(a+1)10-2a>0,解不等式得实数a的取值范围是.【答案】D(4)设a=,b=,c=,则a,b,c的大小关系是________.【解析】 y=x(x>0)为增函数,∴a>c. y=(x∈R)为减函数,∴c>b.∴a>c>b.【答案】a>c>b【小结】(1)幂函数的形式是y=xα(α∈R),其中只有一个参数α,因此只需一个条件即可确定其解析式.(2)若幂函数y=xα(α∈R)是偶函数,则α必为偶数.当α是分数时,一般将其先化为根式,再判断.(3)若幂函数y=xα在(0,+∞)上单调递增,则α>0;若在(0,+∞)上单调递减,则α<0.考点2二次函数的解析式的求法已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,试确定此二次函数的解析式.【解析】法一(利用一般式):设f(x)=ax2+bx+c(a≠0).由题意得解得∴所求二次函数的解析式为f(x)=-4x2+4x+7.法二(利用顶点式):设f(x)=a(x-m)2+n. f(2)=f(-1),∴抛物线的对称轴为x==.∴m=.又根据题意函数有最大值8,∴n=8.∴y=f(x)=a+8. f(2)=-1,∴a+8=-1,解得a=-4,∴f(x)=-4+8=-4x2+4x+7.法三(利用零点式):由已知f(x)+1=0的两根为x1=2,x2=-1,故可设f(x)+1=a(x-2)(x+1),即f(x)=ax2-ax-2a-1.又函数有最大值ymax=8,即=8.解得a=-4或a=0(舍).∴所求函数的解析式为f(x)=-4x2+4x+7.【小结】求二次函数解析式的方法考点3二次函数的图象与性质已知函数f=x2-2ax+5.(1)若f的定义域和...