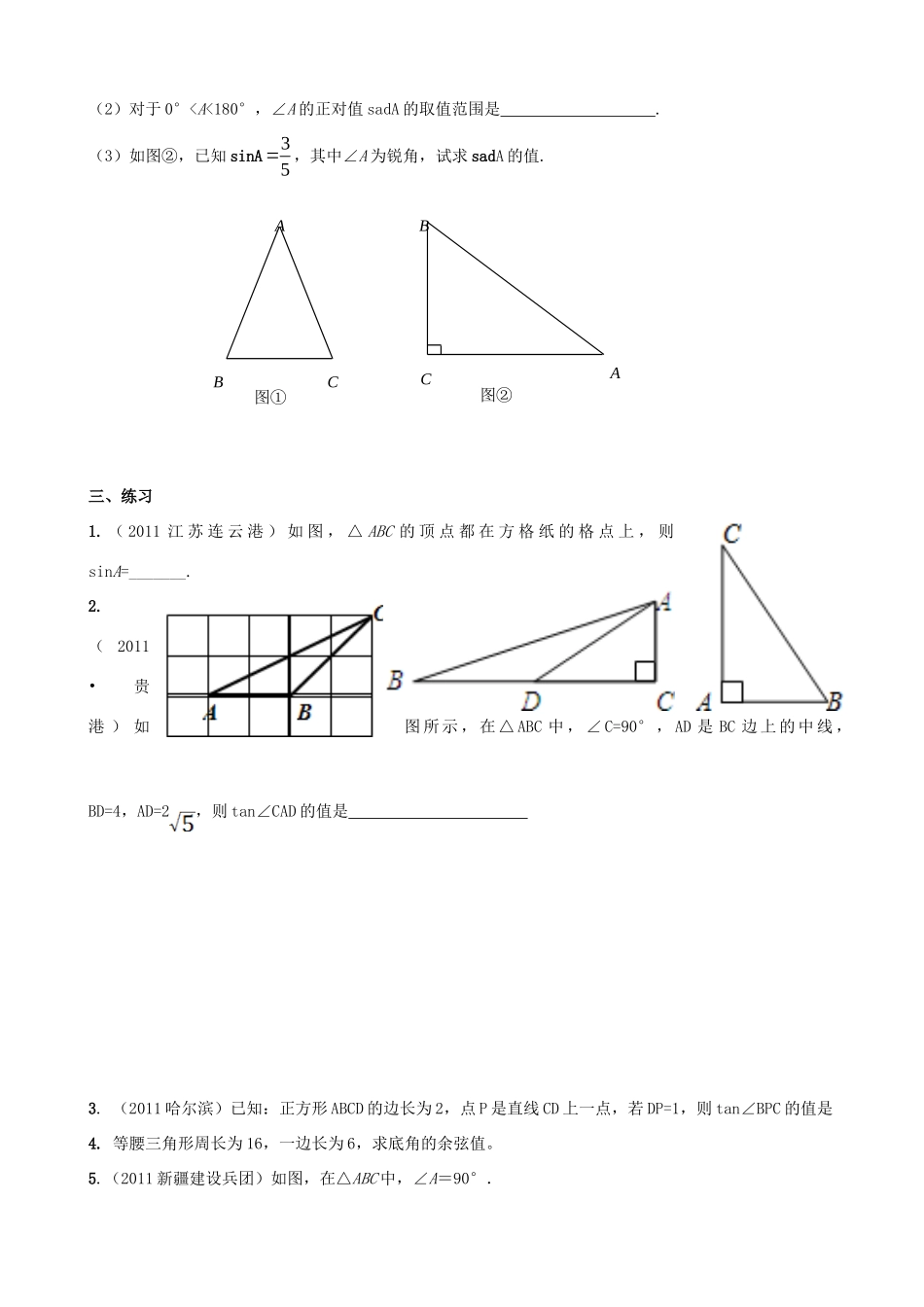
数学:《正弦与余弦》习题(苏科版九年级下)一、复习练习1、在Rt△ABC中,∠C=90°,分别写出∠A的三角函数关系式:sinA=_____,cosA=_____,tanA=_____。∠B的三角函数关系式。2、①在Rt△ABC中,∠C=90°,BC=6,AC=8,则sinA=_____,cosA=_____,tanA=_____。②在Rt△ABC中,∠C=90°,BC=2,AC=4,则sinB=_____,cosB=_____,tanB=_____。③在Rt△ABC中,∠B=90°,AC=2BC,则sinC=_____。④在Rt△ABC中,∠C=90°,AB=10,sinA=53,则BC=_____。⑤在Rt△ABC中,∠C=90°,AB=10,sinB=54,则AC=_____。⑥在Rt△ABC中,∠B=90°,AC=15,sinC=53,则AB=_____。⑦在Rt△ABC中,∠C=90°,cosA=32,AC=12,则AB=_____,BC=_____。二、例题例.1在△ABC中,∠C=90°,cosB=1312,AC=10,求△ABC的周长和斜边AB边上的高例2.(2011四川雅安)已知△ABC的外接圆O的半径为3,AC=4,则sinB=例3.(2011甘肃兰州)通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似的,可以在等腰三角形中建立边角之间的联系。我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图①在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadABCAB底边腰.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:(1)sad60°=.(2)对于0°