正弦函数，余弦函数的图像VIP免费

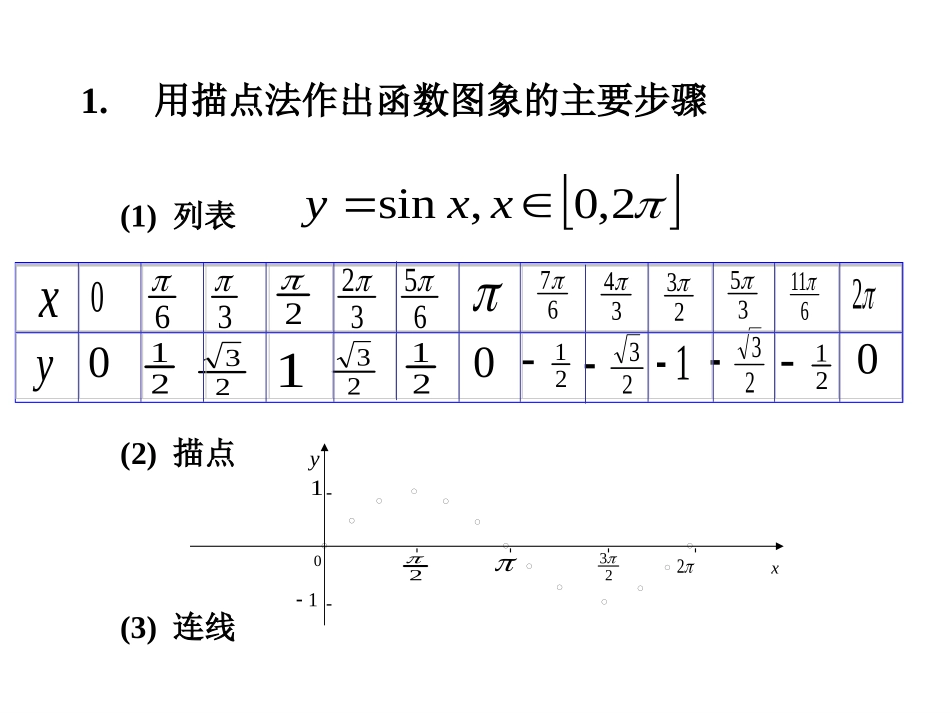
1.4.1正弦函数、余弦函数的图象“简谐运动”实验(1)列表(2)描点(3)连线632326567342335611202123012123212300212312,0,sinxxy1.用描点法作出函数图象的主要步骤---223xy0211---xysinα、cosα的几何意义.正弦线MP余弦线OMoxy11PM想一想?三角问题几何问题2.复习：三角函数线2.函数2,0,sinxxy图象的几何作法....利用三角函数线作三角函数图象223xy11-----02-描点法:查三角函数表得三角函数值,描点,连线.)sin,(xx查表8660.0sin3y如:3x描点)8660.0,(3几何法：作三角函数线得三角函数值，描点)sin,(xx,连线作如:3x3的正弦线,MP平移定点),(MPxPM31Oxy几何法作图的关键是如何利用单位圆中角x的正弦线，巧妙地移动到直角坐标系内，从而确定对应的点(x,sinx).函数2,0,sinxxy图象的几何作法1-1022322656723352yx●●●y=sinx(x[0,])2332346116633265●●●●●●●673435611●●●正弦函数的图象x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线yxo1-122322x6yo--12345-2-3-41正弦、余弦函数的图象余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线正弦曲线形状完全一样只是位置不同正弦函数的图象yxo1-122322如何作出正弦函数的图象（在精确度要求不太高时）？(0,0)(,1)2(,0)(,-1)23(2,0)五点画图法五点法——(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)与x轴的交点)0,(2)0,(23图象的最高点)1,0()1,2(图象的最低点)1,(探究:找出余弦函数的五个关键点简图作法：(1)列表(列出对图象形状起关键作用的五点坐标)(3)连线(用光滑的曲线顺次连结五个点)(2)描点(定出五个关键点)xcosx02322oxy22321-111100例1．画出下列函数的简图（1）y=1+sinx,x∈[0,2π]列表描点作图-2223211-xyo-xxsin1sinx101010210102232（2）y=－cosx,x∈[0,2π]解:(1)]2,0[,sin1xxy]2,0[,sinxxy2-22311xyo-(2)xxcosxcos0223210-101-1010-1]2,0[,cosxxy]2,0[,cosxxy与x轴的交点图象的最高点图象的最低点小结：正弦函数、余弦函数图象的五点法)0,0()0,()0,2()1,(232(,1))0,(2)0,(23)1,0()1,2((1)列表(列出对图象形状起关键作用的五点坐标)(2)描点(定出五个关键点)(3)连线(用光滑的曲线顺次连结五个点)图象的最高点与x轴的交点图象的最低点xysinxycos1，