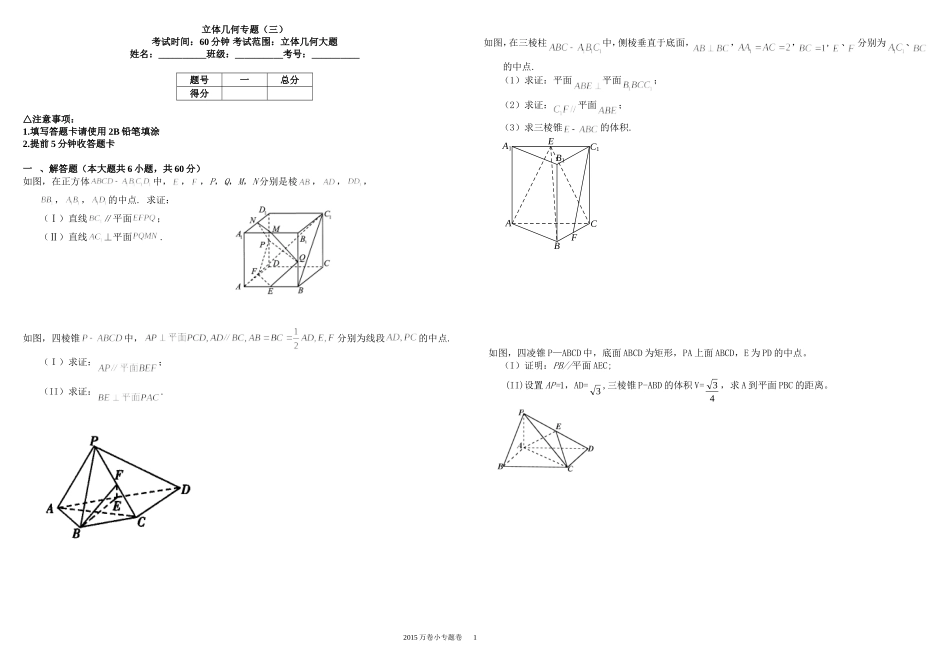
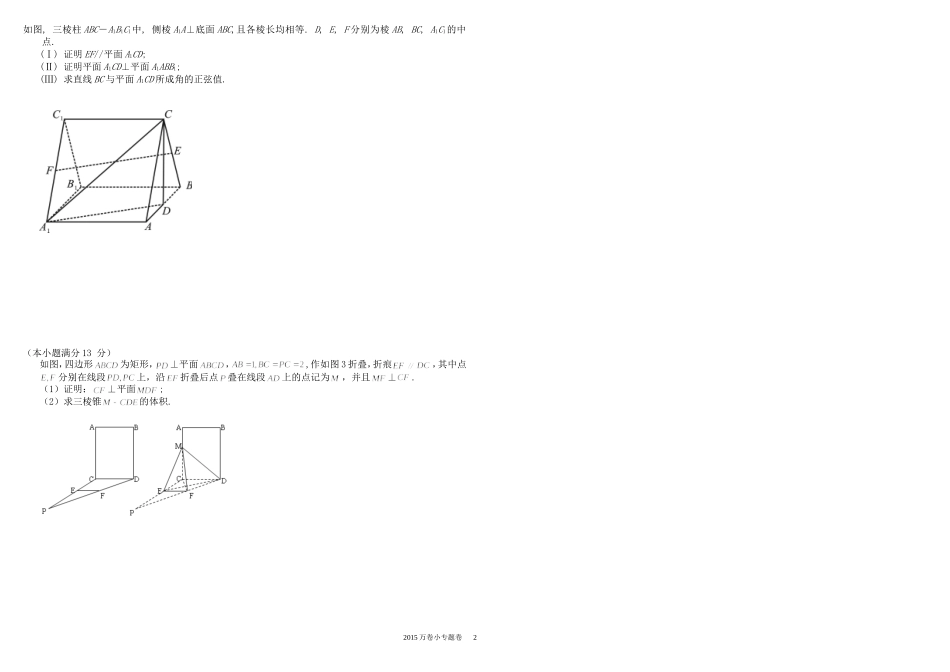
立体几何专题(三)考试时间:60分钟考试范围:立体几何大题姓名:__________班级:__________考号:__________题号一总分得分△注意事项:1.填写答题卡请使用2B铅笔填涂2.提前5分钟收答题卡一、解答题(本大题共6小题,共60分)如图,在正方体中,,,P,Q,M,N分别是棱,,,,,的中点.求证:(Ⅰ)直线∥平面;(Ⅱ)直线⊥平面.如图,四棱锥中,分别为线段的中点.(I)求证:;(II)求证:.如图,在三棱柱中,侧棱垂直于底面,,,,、分别为、的中点.(1)求证:平面平面;(2)求证:平面;(3)求三棱锥的体积.C1B1A1FECBA如图,四凌锥P—ABCD中,底面ABCD为矩形,PA上面ABCD,E为PD的中点。(I)证明:PB//平面AEC;(II)设置AP=1,AD=3,三棱锥P-ABD的体积V=43,求A到平面PBC的距离。2015万卷小专题卷1如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.(Ⅰ)证明EF//平面A1CD;(Ⅱ)证明平面A1CD⊥平面A1ABB1;(Ⅲ)求直线BC与平面A1CD所成角的正弦值.(本小题满分13分)如图,四边形为矩形,⊥平面,,作如图3折叠,折痕,其中点分别在线段上,沿折叠后点叠在线段上的点记为,并且⊥.(1)证明:⊥平面;(2)求三棱锥的体积.2015万卷小专题卷2立体几何专题(三)答案解析一、解答题证明:(Ⅰ)连接AD1,由是正方体,知AD1∥BC1,因为,分别是,的中点,所以FP∥AD1.从而BC1∥FP.而平面,且平面,故直线∥平面.(Ⅱ)如图,连接,,则.由平面,平面,可得.又,所以平面.而平面,所以.因为M,N分别是,的中点,所以MN∥BD,从而.同理可证.又,所以直线⊥平面.证明:(1)设连接OF,EC由于E为AD的中点,所以AE//BC,AE=AB=BC,因此四边形ACBE为菱形,所以O为AC的中点又F为PC的中点因此在△PAC中,可得AP//OF.又平面BEF,平面BEF所以AP//平面BEF(Ⅱ)由题意知所以四边形BCDE为平行四边形,因此BE//CD.又平面PCD,所以,因此.因为四边形ABCE为菱形,所以.又平面PAC,所以平面PAC.解:(Ⅰ)在三棱柱中,底面.所以.又因为.所以平面.所以平面平面.(Ⅱ)取中点,连结,.因为,分别是,的中点,所以,且.因为,且,所以,且.所以四边形为平行四边形.所以.又因为平面,平面,所以平面.(Ⅲ)因为,,,所以.所以三棱锥的体积.解:(I)连接BD交AC于点O,连结EO。因为ABCD为矩形,所以O为BD的中点。又E为PD的中点,所以EO∥PB。EO平面AEC,PB平面AEC,所以PB∥平面AEC.2015万卷小专题卷3GC1B1A1FECBA(II)作由题设知平面PAB,所以故又,所以A到平面PBC的距离为。(1)如图,在三棱柱Z中,AC∥,且AC=,连接ED,ABC中,D,E分别为AB,BC的中点,DE=,且DE∥ACF为的中点,可得且∥DE即四边形为平行四边形,所以EF∥又EF平面,所以EF∥平面(2)由于底面ABC是正三角形,D为AB的中点,故,又由于侧棱,,CD,所以,又,因此CD平面,而CD,所以平面,(3)在平面内,过点B作BG交直线于点G,连接CG由于平面,而直线是与平面,的交线故BG,由此可得为直线BG与所成的角设棱长为a,可得=,由,易得BG=,在中,所以,直线BC所成的角的正弦值为.2015万卷小专题卷4