九年级数学上册 2911几何问题的处理方法精品同步作业 华东师大版试卷VIP免费

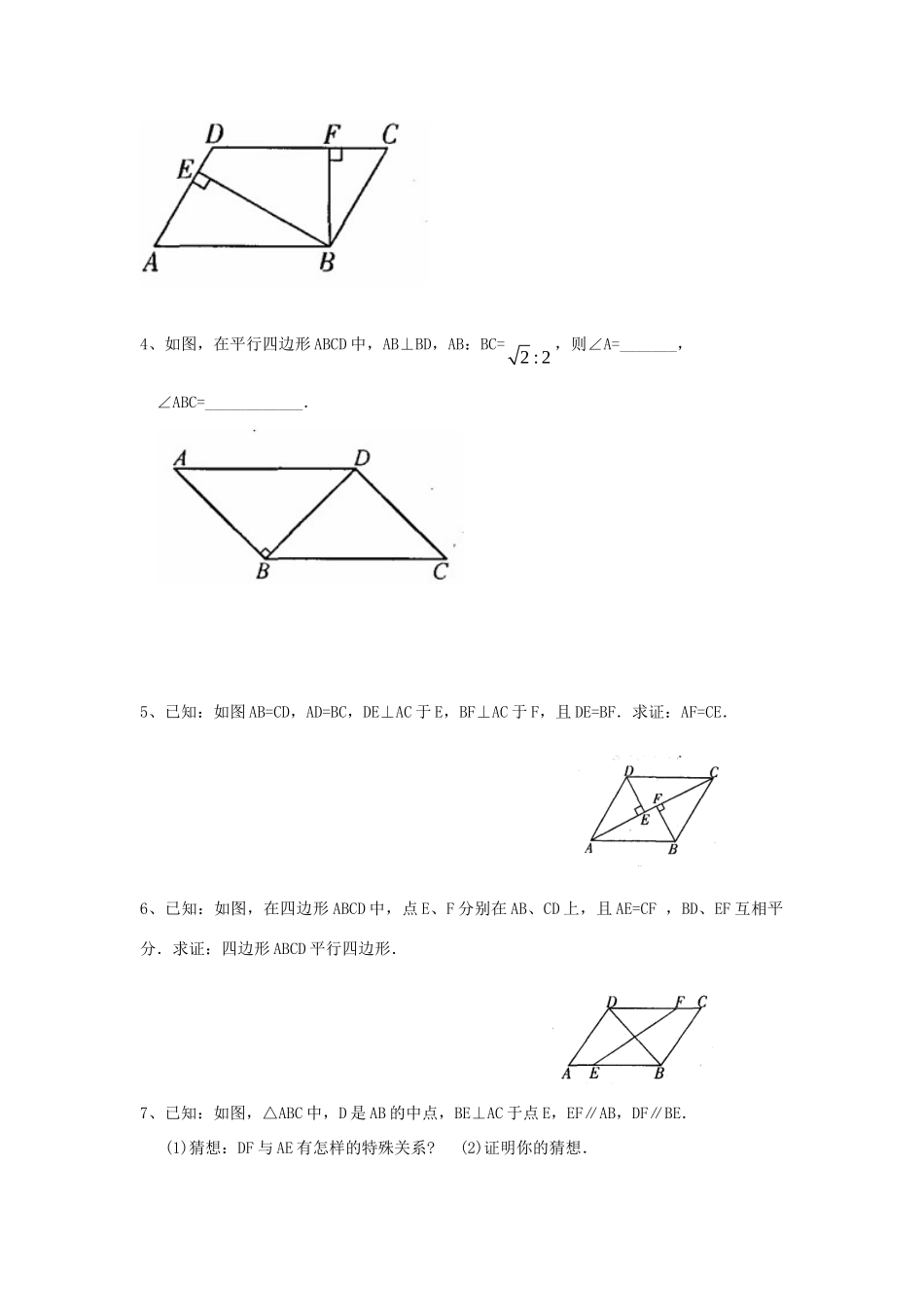
29.1.1几何问题处理方法◆随堂检测1、任何一个三角形的外角和都是__________度．2、如图，∠A=50°，∠ABD=28°，∠ACO=32°，则∠BDC=____度，∠BOC=___度．3、在平行四边形ABCD中，若∠A+∠C=160°，则∠A=________°，∠B=_________°．4、已知平行四边形ABCD的周长是30cm，AB：BC=3：2，则AB=_______cm，BC=______cm．5、如图，∠ABC=∠ACB，BE、CD分别为∠ABC，∠ACB的平分线，则∠ADC与∠AEB的大小关系是()A．∠ADC>∠AEBB．∠ADC=∠AEBC．∠ADC<∠AEBD．不确定◆典例分析如图，在□ABCD中，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．（1）试说明：AE⊥BF；（2）判断线段DF与CE的大小关系，并予以说明．分析：（1）利用“两直线平行，同旁内角互补”可知0180DABABC，再利用角平分线的就可以很容易得证；（2）平行线与角平分线搭配可以得到等腰三角形是一种常见的配合，已知△ADE和△BCF是等腰三角形，易得DE=CF.解：（1） 在ABCD中，AD∥BC∴∠DAB＋∠ABC＝180° AE、BF分别平分∠DAB和∠ABC∴∠DAB＝2∠BAE，∠ABC＝2∠ABF∴2∠BAE＋2∠ABF＝180°MFEDCBA即∠BAE＋∠ABF＝90°∴∠AMB＝90°∴AE⊥BF．(2)线段DF与CE是相等关系，即DF＝CE 在ABCD中，CD∥AB∴∠DEA＝∠EAB又 AE平分∠DAB∴∠DAE＝∠EAB∴∠DEA＝∠DAE∴DE＝AD同理可得，CF＝BC又 在ABCD中，AD＝BC∴DE＝CF∴DE－EF＝CF－EF即DF＝CE．◆课下作业●拓展提高1、直角三角形斜边上的中线同时又是斜边上的高，则此直角三角形的两锐角关系是()A．相等B．一个角90°，一个角30°C．互补D．互余但不等2、如图，在平行四边形ABCD中，EF∥AD，MN∥AB，EF、MN相交于点P，则除平行四边形ABCD外，图中共有平行四边形()A．4个B．6个C．8个D．10个3、如图，在平行四边形ABCD中，∠A=60°，BE⊥AD，BF⊥CD，E、F是垂足，AB=8cm，BC=4cm，则∠D=________°，∠EBF=________°，BE=_________cm，BF=_________cm，ABCDS=________cm2．4、如图，在平行四边形ABCD中，AB⊥BD，AB：BC=2:2，则∠A=_______，∠ABC=____________．5、已知：如图AB=CD，AD=BC，DE⊥AC于E，BF⊥AC于F，且DE=BF．求证：AF=CE．6、已知：如图，在四边形ABCD中，点E、F分别在AB、CD上，且AE=CF，BD、EF互相平分．求证：四边形ABCD平行四边形．7、已知：如图，△ABC中，D是AB的中点，BE⊥AC于点E，EF∥AB，DF∥BE．(1)猜想：DF与AE有怎样的特殊关系?(2)证明你的猜想．●体验中考1、（2009年崇左）一个等腰三角形的两边长分别为2和5，则它的周长为（）A．7B．9C．12D．9或122、（2009年湖南怀化）如图，在RtABC△中，90B，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知10BAE，则C的度数为（）A．30B．40C．50D．603、(2009年陕西省)如图，在□ABCD中，点E是AD的中点，连接CE并延长，交BA的延长线于点F．求证：FA＝AB．4、(2009年云南省)如图，在△ABC和△DCB中，AB=DC，AC=DB，AC与DB交于点M．（1）求证：△ABC≌△DCB；（2）过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N，试判断线段BN与CN的数量关系，并证明你的结论．参考答案：◆随堂检测1、1800ADCEBBCADMN2、780，1100（提示：三角形外角性质）3、800，1000（提示：平行四边形的对角相等，邻角互补）4、9，6（提示：设AB=3x，BC=2x）5、B（提示：利用三角形外角性质）◆课下作业●拓展提高1、A（等腰三角形的“三线合一”）2、C3、1200，600，43，23，163（提示：利用平行四边形的邻角互补可求得∠D=1200）4、450，1350（提示：利用三角函数）5、证明： AB=CD，AD=BC，∴四边形ABCD是平行四边形，∴AB=DC， DE⊥AC于E，BF⊥AC于F∴∠AFB=∠CED=900在△ABF和△CDE中， DE=BF，DC=AB，∴△ABF≌△CDE∴AF=CE6、证明：连接DE，BE BD、EF互相平分∴四边形BEDF是平行四边形∴DF∥BE，DF=EB AE=FC∴AB=DC∴四边形ABCD平行四边形7、解：DF、AE互相垂直平分。证明： EF∥AB，DF∥BE∴四边形DBEF是平行四边形∴EF∥AB即EF∥AD，BD=EF D是AB的中点∴AD=BD∴AD=EF∴四边形ADEF是平行四边形 DF∥BE，BE⊥AC∴DF⊥AC∴平行四边形ADEF是菱形...