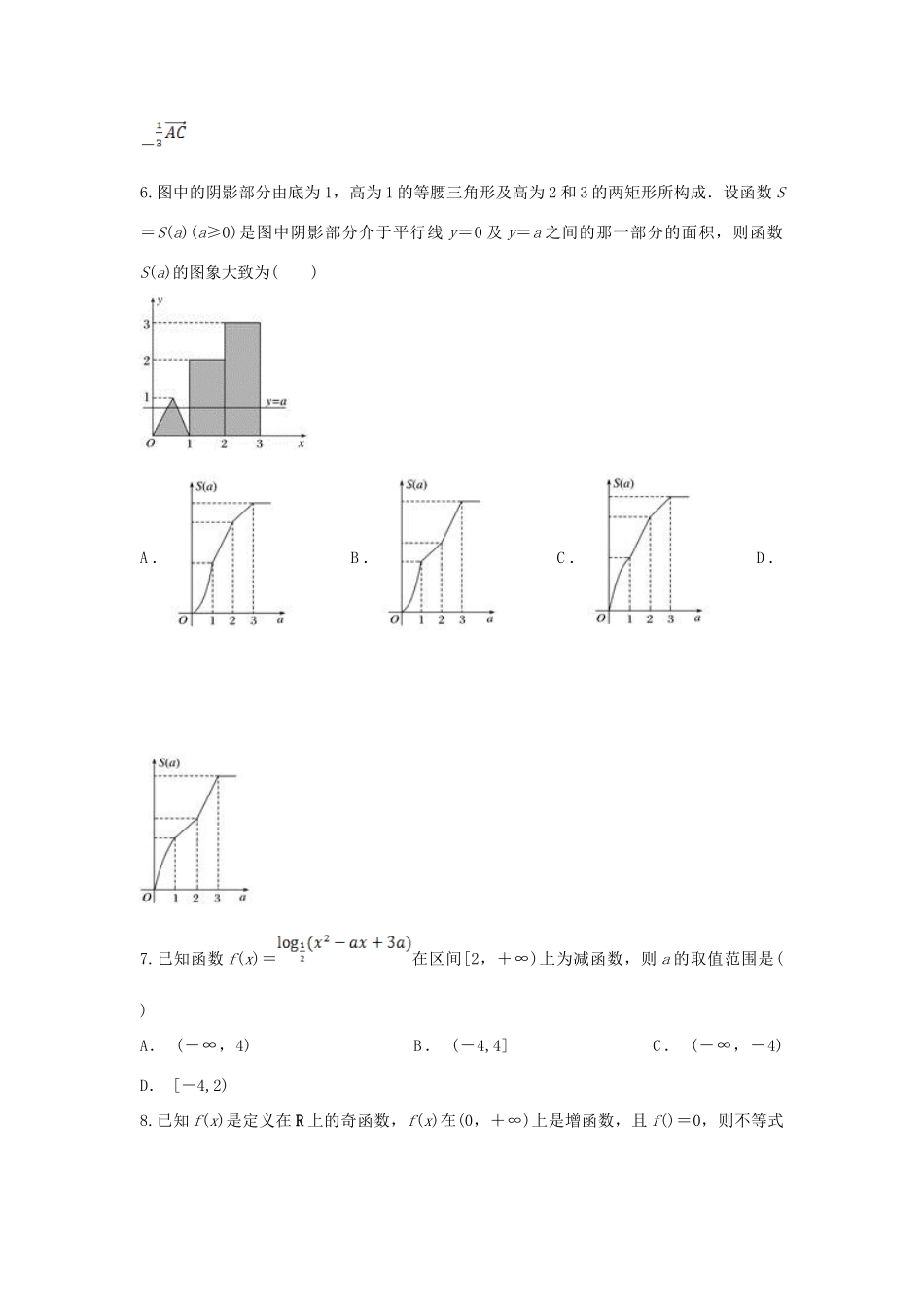
育才学校2019-2020学年度第一学期期末考试高一实验班数学一、选择题(共12小题,每小题5分,共60分)1.若函数y=f(x)的值域是[,3],则函数F(x)=f(x)+的值域是()A.[,3]B.[2,]C.[,]D.[3,]2.定义在R上偶函数f(x)在[1,2]上是增函数,且具有性质f(1+x)=f(1-x),则函数f(x)()A.在[-1,0]上是增函数B.在[-1,-]上增函数,在(-,0]上是减函数C.在[1,0]上是减函数D.在[-1,-]上是减函数,在(-,0]上是增函数3.已知g(x)=ax+a,f(x)=对任意x1∈[-2,2],存在x2∈[-2,2],使g(x1)=f(x2)成立,则a的取值范围是()A.[-1,+∞)B.[-,1]C.(0,1]D.(-∞,1]4.已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)等于()A.-3B.-1C.1D.35.设D为△ABC所在平面内一点,且满足=3,则()A.=-+B.=-C.=+D.=-6.图中的阴影部分由底为1,高为1的等腰三角形及高为2和3的两矩形所构成.设函数S=S(a)(a≥0)是图中阴影部分介于平行线y=0及y=a之间的那一部分的面积,则函数S(a)的图象大致为()A.B.C.D.7.已知函数f(x)=在区间[2,+∞)上为减函数,则a的取值范围是()A.(-∞,4)B.(-4,4]C.(-∞,-4)D.[-4,2)8.已知f(x)是定义在R上的奇函数,f(x)在(0,+∞)上是增函数,且f()=0,则不等式f()<0的解集为()A.(0,)B.(,+∞)C.(,1)∪(2,+∞)D.(0,)∪(2,+∞)9.已知向量=(1,-3),=(2,-1),=(k+1,k-2),若A,B,C三点不能构成三角形,则实数k应满足的条件是()A.k=-2B.k=C.k=1D.k=-110.已知ω>0,函数f(x)=sin在上单调递减,则ω的取值范围是()A.B.C.D.(0,2]11.函数y=Asin(ωx+φ)在一个周期内的图象如图所示,则此函数的解析式为()A.y=2sinB.y=2sinC.y=2sinD.y=2sin12.已知菱形ABCD的边长为a,∠ABC=60°,则·等于()A.-a2B.-a2C.a2D.a2二、填空题(共4小题,每小题5分,共20分)13.已知sin+sinα=-,-<α<0,则cosα=________.14.已知函数f(x)满足对任意的x∈R,都有f(+x)+f(-x)=2,则f()+f()+…+f()=________.15.已知函数y=f(x)是奇函数,当x<0时,f(x)=x2+ax(a∈R),且f(2)=6,则f(1)=________.16.函数f(x)=-2sin2x+sin2x+1,给出下列四个命题:①在区间上是减函数;②直线x=是函数图象的一条对称轴;③函数f(x)的图象可由函数y=sin2x的图象向左平移而得到;④若x∈,则f(x)的值域是[0,].其中正确命题序号是________.三、解答题(共6小题,共70分)17.(12分)函数f(x)的定义域为D={x|x≠0},且满足对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2).(1)求f(1)的值;(2)判断f(x)的奇偶性并证明你的结论;(3)如果f(4)=1,f(x-1)<2,且f(x)在(0,+∞)上是增函数,求x的取值范围.18.(12分)已知函数f(x)=log2(2x+1).(1)求证:函数f(x)在(-∞,+∞)内单调递增;(2)若g(x)=log2(2x-1)(x>0),且关于x的方程g(x)=m+f(x)在[1,2]上有解,求m的取值范围.19.(10分)已知=(-1,3),=(3,m),=(1,n),且∥.(1)求实数n的值;(2)若⊥,求实数m的值.20.(12分)已知函数f(x)=2sin+a,a为常数.(1)求函数f(x)的最小正周期;(2)求函数f(x)的单调递增区间;(3)若x∈时,f(x)的最小值为-2,求a的值.21.(12分)平面内有向量=(1,7),=(5,1),=(2,1),点Q为直线OP上的一个动点.(1)当·取最小值时,求的坐标;(2)当点Q满足(1)的条件和结论时,求cos∠AQB的值.22.(12分)已知sin(A+)=,A∈(,).(1)求cosA的值;(2)求函数f(x)=cos2x+sinAsinx的值域.参考答案1-5BABCA6-10CBCCA11-12AD13.14.715.416.①②17.(1) 对于任意x1,x2∈D,有f(x1·x2)=f(x1)+f(x2),∴令x1=x2=1,得f(1)=2f(1),∴f(1)=0.(2)f(x)为偶函数.证明:令x1=x2=-1,有f(1)=f(-1)+f(-1),∴f(-1)=f(1)=0.令x1=-1,x2=x有f(-x)=f(-1)+f(x),∴f(-x)=f(x),∴f(x)为偶函数.(3)依题设有f(4×4)=f(4)+f(4)=2,由(2)知,f(x)是偶函数,∴f(x-1)<2⇔f(|x-1|)