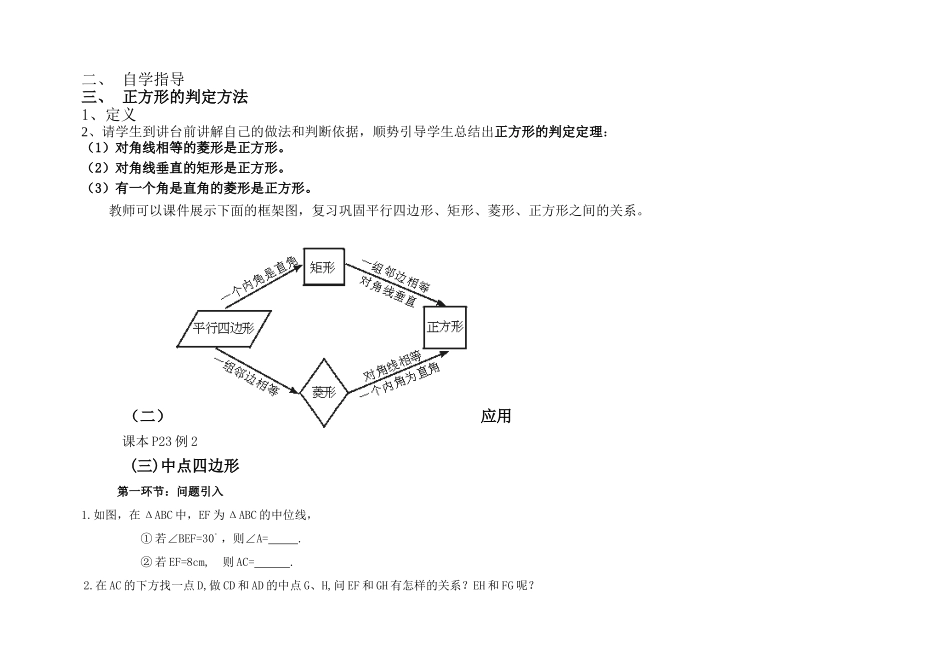
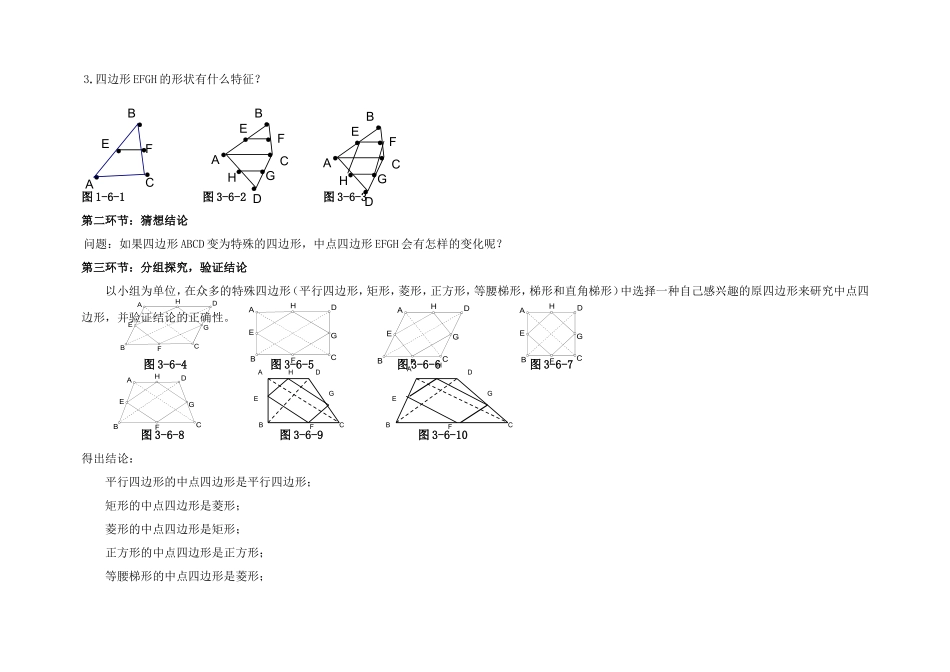
桥山中学2014-2015学年度第一学期九年级数学教案主备人:程雪玲副备人:刘苗苗周次星期星期班级九(十一、二)课题正方形的性质与判定(3)课时1学习目标1.掌握正方形的判定定理,并能综合运用特殊四边形的性质和判定解决问题。2.经历“探索—发现—猜想—证明”的过程,发现决定中点四边形形状的因素,熟练运用特殊四边形的性质及判定对中点四边形进行判断,并能对自己的猜想进行证明,进一步发展学生演绎推理的能力。3.进一步体会证明的必要性以及计算与证明在解决问题中的作用。重点内容解决措施理解矩形的判定定理,培养分析思路教师引导自主练习合作交流练习提高难点培养几何推理能力,形成分析思路教师引导自主练习合作交流教学方法自主交流,讨论探究课前准备课件三角尺直尺情境导入将一张长方形纸对折两次,然后剪下一个角,打开,怎样剪才能剪出一个正方形?一、出示学习目标二、自学指导三、正方形的判定方法1、定义2、请学生到讲台前讲解自己的做法和判断依据,顺势引导学生总结出正方形的判定定理:(1)对角线相等的菱形是正方形。(2)对角线垂直的矩形是正方形。(3)有一个角是直角的菱形是正方形。教师可以课件展示下面的框架图,复习巩固平行四边形、矩形、菱形、正方形之间的关系。(二)应用课本P23例2(三)中点四边形第一环节:问题引入1.如图,在ΔABC中,EF为ΔABC的中位线,①若∠BEF=30°,则∠A=.②若EF=8cm,则AC=.2.在AC的下方找一点D,做CD和AD的中点G、H,问EF和GH有怎样的关系?EH和FG呢?3.四边形EFGH的形状有什么特征?图1-6-1图3-6-2图3-6-3第二环节:猜想结论问题:如果四边形ABCD变为特殊的四边形,中点四边形EFGH会有怎样的变化呢?第三环节:分组探究,验证结论以小组为单位,在众多的特殊四边形(平行四边形,矩形,菱形,正方形,等腰梯形,梯形和直角梯形)中选择一种自己感兴趣的原四边形来研究中点四边形,并验证结论的正确性。图3-6-4图3-6-5图3-6-6图3-6-7图3-6-8图3-6-9图3-6-10得出结论:平行四边形的中点四边形是平行四边形;矩形的中点四边形是菱形;菱形的中点四边形是矩形;正方形的中点四边形是正方形;等腰梯形的中点四边形是菱形;FECABCGHFEDABCGHFEDABABCDEFGHABCDEFGHABCDEFGHABCDEFGHABCDEFGHABCDEFGHABCDEFGH直角梯形的中点四边形是平行四边形;梯形的中点四边形是平行四边形。问题:1.矩形和等腰梯形是形状不同的四边形,为什么中点四边形都由平行四边形变化为菱形?2.平行四边形变化为菱形需要增加什么条件?3.你是从什么角度考虑的?4.你从哪儿得到的启发?5.你能用你的发现解释其它的图形变化吗?例如:原四边形为菱形,其中点四边形为矩形?概括出规律:决定中点四边形EFGH的形状的主要因素是原四边形ABCD的对角线的长度和位置关系。(1)若对角线相等,则中点四边形EFGH为菱形;(2)若对角线互相垂直,则中点四边形EFGH为矩形;(3)若对角线既相等,又垂直,则中点四边形EFGH为正方形;(4)若对角线既不相等,又不垂直,则中点四边形EFGH为平行四边形。图3-6-11图3-6-12图3-6-13图3-6-14运用巩固1、图形发散练习BCDAHGFEBCDAHGFEBCDAHGFEBCDAHGFE利用几何画板,拖动A点使四边形ABCD的图形变化进行研究。图3-6-15图3-6-16图3-6-17图3-6-182、应用拓展练习1.四边形ABCD中,AC=6,BD=8,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1;再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2……如此进行下去得到四边形AnBnCnDn。(1)证明:四边形A1B1C1D1是矩形;(2)写出四边形A1B1C1D1和四边形A2B2C2D2的面积;(3)写出四边形AnBnCnDn的面积;(4)求四边形A5B5C5D5的周长。2.如图,矩形ABCD的长为4,宽为3,连续取三次中点后的最小四边形的面积为多少?CABD图3-6-19练习2的拓展:(1)若上题连续取n次中点后的最小四边形AnBnCnDn的面积为多少呢?ABCDEFGHABCDEFGHABCDEFGHABCDEFGH(2)若上题改为菱形,边长为4,连续取n次中点后的最小四边形AnBnCnDn的面积为多少呢?(3)若上题改为正方形,边长为4,连续取n次中点后的最小四边形AnBnCnDn的面积为多少呢?(4)若以上题目改为求连续取n次中点...