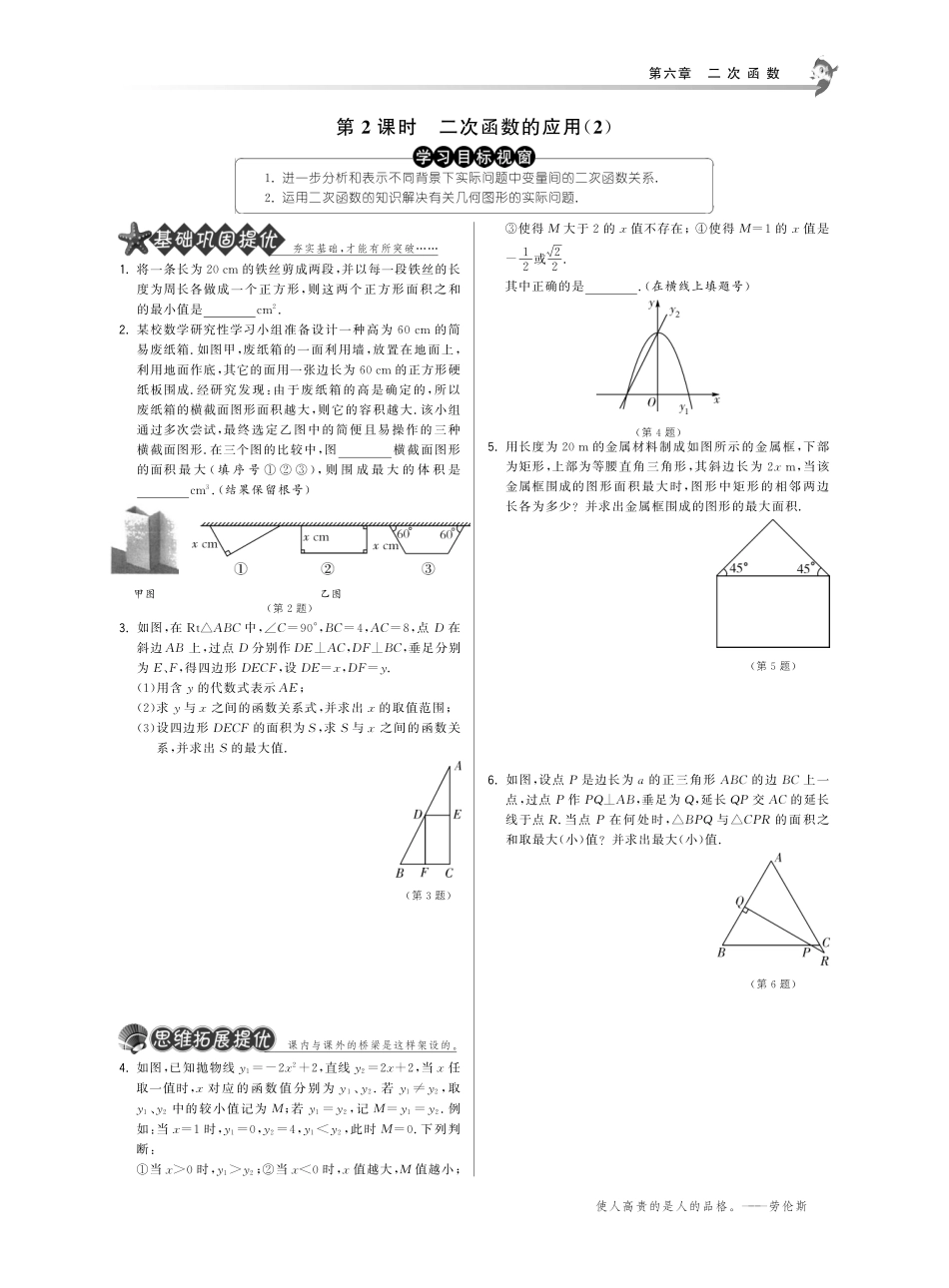
第六章二次函数使人高贵的是人的品格.———劳伦斯第2课时二次函数的应用(2)1.进一步分析和表示不同背景下实际问题中变量间的二次函数关系.2.运用二次函数的知识解决有关几何图形的实际问题.夯实基础,才能有所突破1.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是cm2.2.某校数学研究性学习小组准备设计一种高为60cm的简易废纸箱.如图甲,废纸箱的一面利用墙,放置在地面上,利用地面作底,其它的面用一张边长为60cm的正方形硬纸板围成.经研究发现:由于废纸箱的高是确定的,所以废纸箱的横截面图形面积越大,则它的容积越大.该小组通过多次尝试,最终选定乙图中的简便且易操作的三种横截面图形.在三个图的比较中,图横截面图形的面积最大(填序号①②③),则围成最大的体积是cm3.(结果保留根号)甲图乙图(第2题)3.如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,过点D分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.(1)用含y的代数式表示AE;(2)求y与x之间的函数关系式,并求出x的取值范围;(3)设四边形DECF的面积为S,求S与x之间的函数关系,并求出S的最大值.(第3题)课内与课外的桥梁是这样架设的.4.如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:①当x>0时,y1>y2;②当x<0时,x值越大,M值越小;③使得M大于2的x值不存在;④使得M=1的x值是-12或22.其中正确的是.(在横线上填题号)(第4题)5.用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2xm,当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?并求出金属框围成的图形的最大面积.(第5题)6.如图,设点P是边长为a的正三角形ABC的边BC上一点,过点P作PQ⊥AB,垂足为Q,延长QP交AC的延长线于点R.当点P在何处时,△BPQ与△CPR的面积之和取最大(小)值?并求出最大(小)值.(第6题)惟有真才能血性,须从本色见英雄.———黄兴对未知的探索,你准行!7.如图,已知正方形ABCD的边长为4,点E是BC边上的一个动点,AE⊥EF,EF交DC于点F,设BE=x,FC=y,则当点E从点B运动到点C时,y关于x的函数图象是().(第7题)8.如图,在直角坐标系中,O是坐标原点,A、B、C三点的坐标分别为A(18,0)、B(18,6)、C(8,6),四边形OABC是梯形.点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位,点Q沿OC、CB向终点B运动,当这两点有一点到达自己的终点时,另一点也停止运动.(1)求出直线OC的解析式及经过O、A、C三点的抛物线的解析式;(2)试在(1)中的抛物线上找一点D,使得以O、A、D为顶点的三角形与△AOC全等,请直接写出点D的坐标;(3)设从点O出发起,运动了t秒,如果点Q的速度为每秒2个单位,试写出点Q的坐标,并写出此时t的取值范围;(4)设从点O出发起,运动了t秒,当P、Q两点运动的路程之和恰好等于梯形OABC周长的一半时,直线PQ能否把梯形的面积也分成相等的两部分?若能,请求出t的值;若不能,请说明理由.(第8题)解剖真题,体验情境.9.(2012山东青岛)在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:(第9题)(1)试判断y与x之间的函数关系,并求出函数关系式;(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.第2课时二次函数的应用(2)1.12.52.③,1800033.(1)由题意可知四边形DECF为矩形,则AE=AC-DF=8-y.(2)由DE∥BC,得DEBC=AEAC,即x4=8-y8,所以y=8-2x.x的取值范围是0<x<4.(3)...