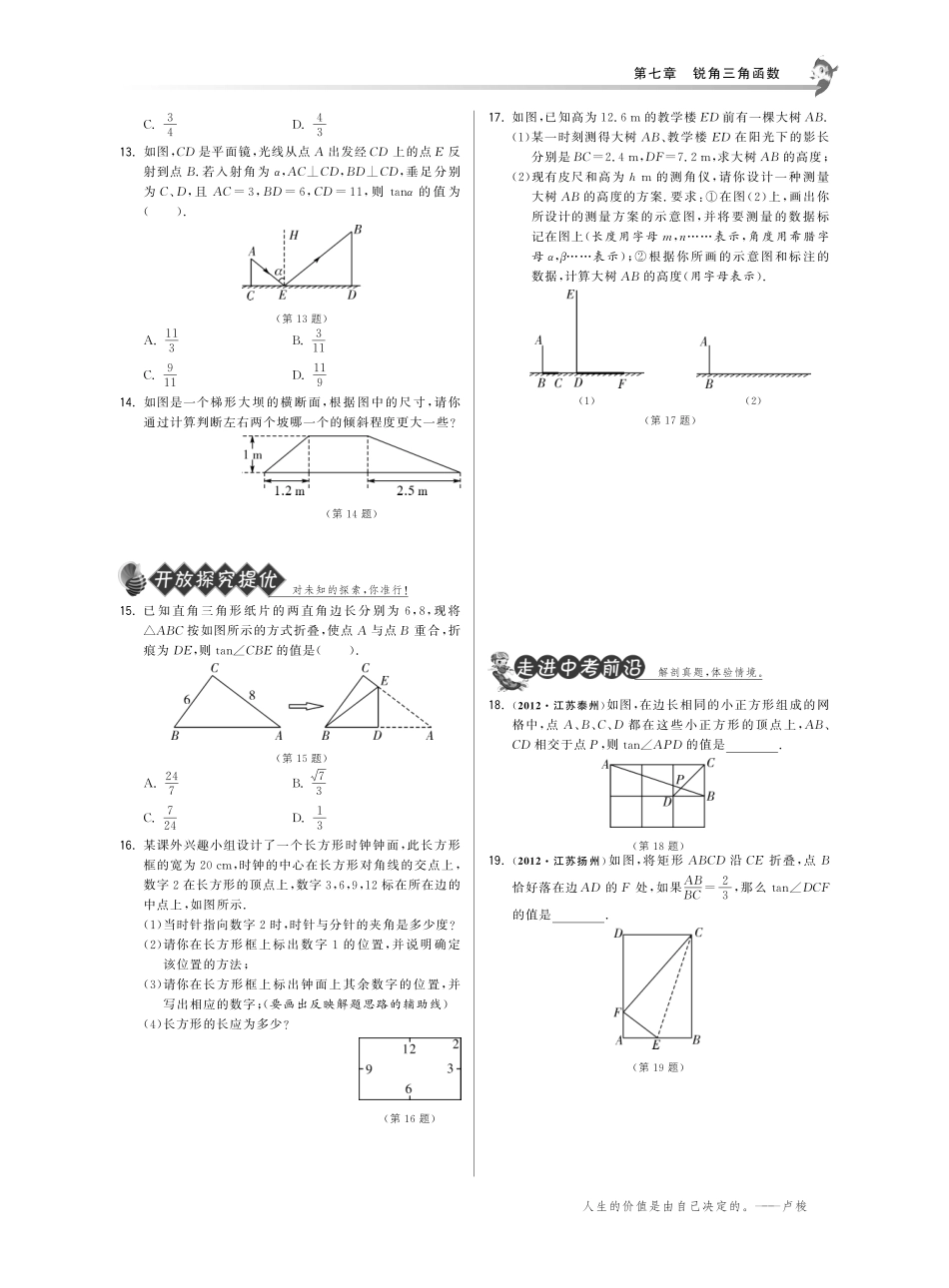
没有任何动物比蚂蚁更勤奋,然而它却最沉默寡言.———富兰克林第七章锐角三角函数7.1正切1.了解正切的概念.2.会根据直角三角形三边的关系求锐角的正切值.3.会用计算器求锐角的正切值.夯实基础,才能有所突破1.在△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a,b,c.(1)若a=3,b=4,则tanA=;(2)若b=21,c=29,则tanA=;(3)若a=2,b=6,则tanA=;(4)若a=9,c=15,则tanA=.2.分别求出图中∠A、∠B的正切值:(其中∠C=90°)(第2题)由上面的例子可以得出结论:直角三角形的两个锐角的正切值互为.3.如图是教学用的直角三角板,边AC=30cm,∠C=90°,tan∠BAC=33,则边BC的长为().A.303cmB.203cmC.103cmD.53cm(第3题)(第4题)4.如图,在正方形ABCD中,点E为AD的中点,连接EB,设∠EBA=α,则tanα=.5.在直角坐标系中,△ABC的三个顶点的坐标分别为A(-4,1)、B(-1,3)、C(-4,3),试求tanB的值.6.求下列直角三角形中字母所表示的值.(第6题)7.在△ABC中,∠C=90°,a∶b=3∶5,求∠A、∠B的正切值.课内与课外的桥梁是这样架设的.8.若等腰三角形的两边长分别为6和8,则底角α的正切值为.9.若∠A是锐角,且关于x的方程3x2-2tanAx+1=0有两个相等的实数根,则∠A的度数为.10.如图,在△ABC中,∠A=30°,tan∠B=32,AC=23,则AB=.(第10题)(第11题)11.如图,∠1的正切值等于.12.如图,AB是☉O的直径,弦CD⊥AB于点E,连接OC.若OC=5,CD=8,则tan∠COE等于().(第12题)A.35B.45第七章锐角三角函数人生的价值是由自己决定的.———卢梭C.34D.4313.如图,CD是平面镜,光线从点A出发经CD上的点E反射到点B.若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C、D,且AC=3,BD=6,CD=11,则tanα的值为().(第13题)A.113B.311C.911D.11914.如图是一个梯形大坝的横断面,根据图中的尺寸,请你通过计算判断左右两个坡哪一个的倾斜程度更大一些?(第14题)对未知的探索,你准行!15.已知直角三角形纸片的两直角边长分别为6,8,现将△ABC按如图所示的方式折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是().(第15题)A.247B.73C.724D.1316.某课外兴趣小组设计了一个长方形时钟钟面,此长方形框的宽为20cm,时钟的中心在长方形对角线的交点上,数字2在长方形的顶点上,数字3,6,9,12标在所在边的中点上,如图所示.(1)当时针指向数字2时,时针与分针的夹角是多少度?(2)请你在长方形框上标出数字1的位置,并说明确定该位置的方法;(3)请你在长方形框上标出钟面上其余数字的位置,并写出相应的数字;(要画出反映解题思路的辅助线)(4)长方形的长应为多少?(第16题)17.如图,已知高为12.6m的教学楼ED前有一棵大树AB.(1)某一时刻测得大树AB、教学楼ED在阳光下的影长分别是BC=2.4m,DF=7.2m,求大树AB的高度;(2)现有皮尺和高为hm的测角仪,请你设计一种测量大树AB的高度的方案.要求:①在图(2)上,画出你所设计的测量方案的示意图,并将要测量的数据标记在图上(长度用字母m,n表示,角度用希腊字母α,β表示);②根据你所画的示意图和标注的数据,计算大树AB的高度(用字母表示).(1)(2)(第17题)解剖真题,体验情境.18.(2012江苏泰州)如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是.(第18题)19.(2012江苏扬州)如图,将矩形ABCD沿CE折叠,点B恰好落在边AD的F处,如果ABBC=23,那么tan∠DCF的值是.(第19题)第七章锐角三角函数7.1正切1.(1)34(2)2021(3)13(4)342.(1)tanA=43,tanB=34(2)tanA=4855,tanB=5548(3)tanA=83,tanB=38倒数3.C4.125.236.(1)a=8,b=43(2)α=30°,β=60°7.tanA=35,tanB=538.553或529.60°提示:Δ=4tan2A-12=0,tan2A=3,tanA=3,所以∠A=60°.10.5提示:过点C作CH⊥AB,垂足为H.在Rt△C...