九年级数学上册 切线性质与判定周测2(pdf) 新人教版试卷VIP免费

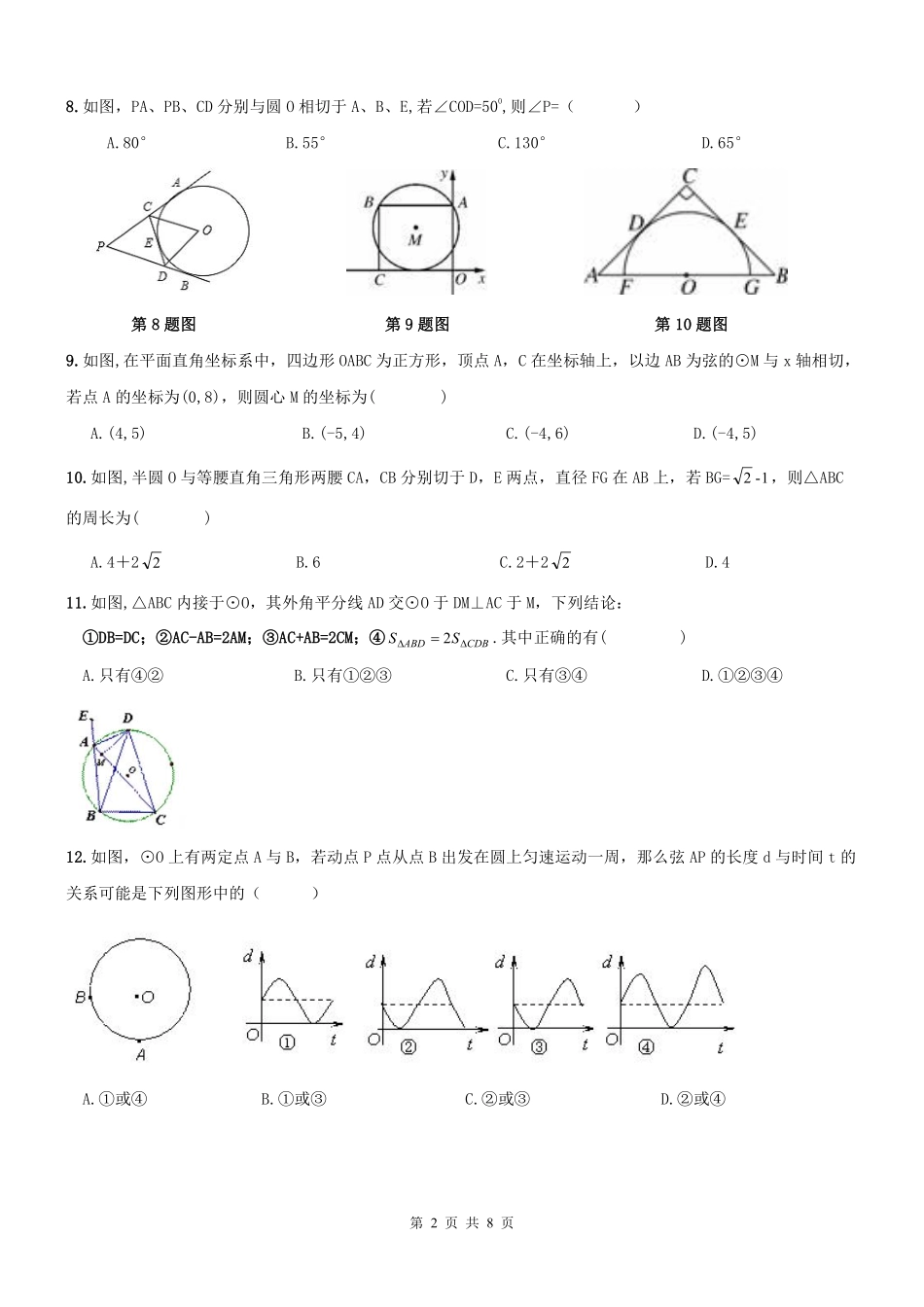
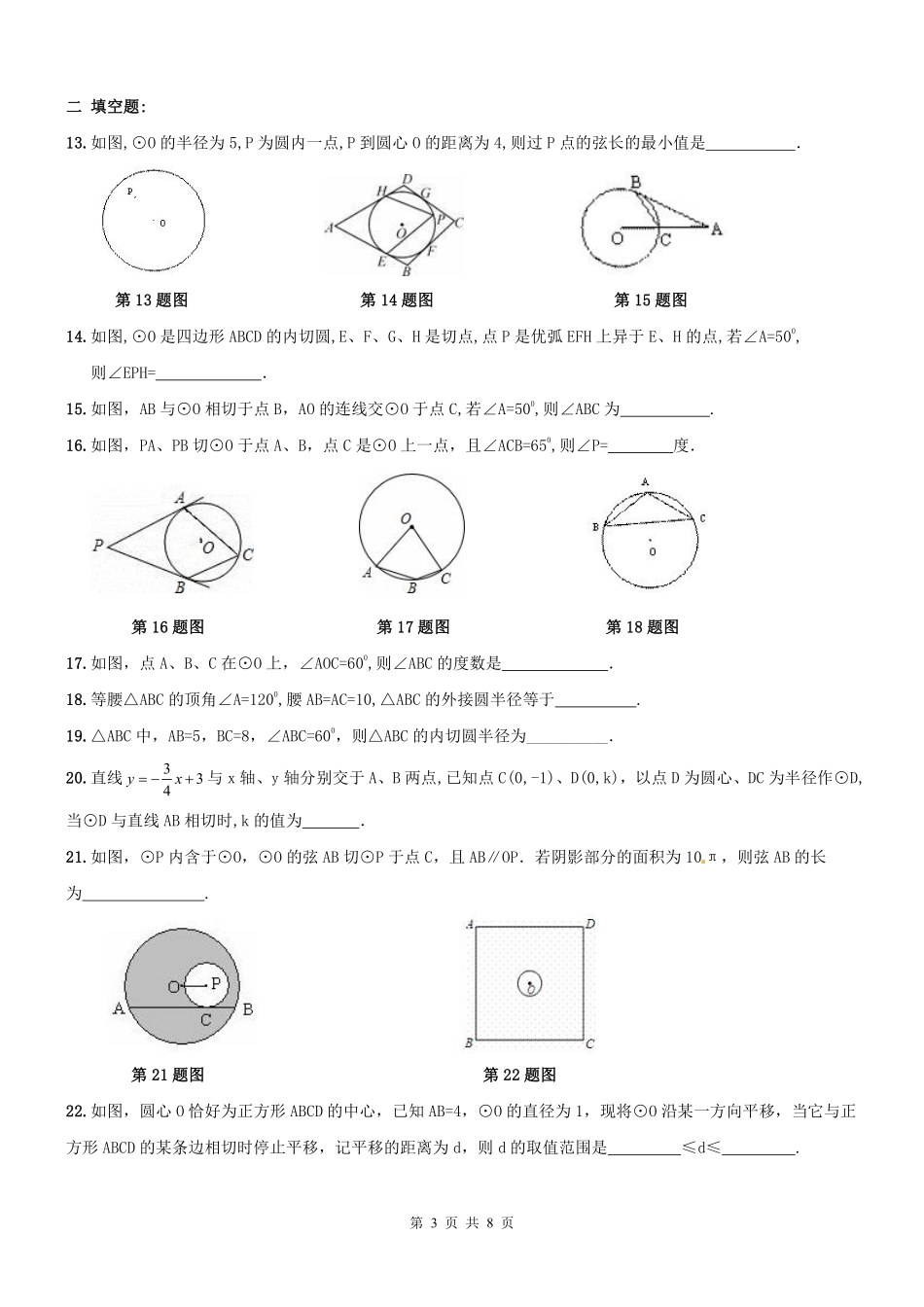
第1页共8页2016-2017学年度第一学期九年级数学切线的性质与判定周测姓名：_______________班级：_______________得分：_______________一选择题：1.已知矩形ABCD的边AB=15,BC=20，以点B为圆心作圆,使A、C、D三点至少有一点在⊙B内,且至少有一点在⊙B外，则⊙B的半径r的取值范围是（）A.r＞15B.15＜r＜20C.15＜r＜25D.20＜r＜252.如图,AB是⊙O的直径,C,D两点在⊙O上,若∠BCD=400,则∠ABD的度数为（）A.40°B.50°C.80°D.90°第2题图第3题图第4题图3.如图,PA与⊙O相切于点A,PO的延长线与⊙O交于点C,若⊙O的半径为3,PA=4.弦AC长为（）A.5B.554C.556D.55124.如图，若点O是△ABC的内心,∠ABC=800,∠ACB=600则∠BOC的度数为()A.140°B.130°C.120°D.110°5.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2，则CE为（）A.6B.13C.8D.213第5题图第6题图第7题图6.如图,⊙O半径为2,AB为⊙O的直径,BC为⊙O的一条弦，若∠ABC=30°,过点C作AB的垂线,垂足为点D,则CD长为（）A.3B.5C.2D.17.如图，圆心在y轴的负半轴上，半径为5的⊙B与y轴的正半轴交于点A(0,1)，过点P(0,-7)的直线l与⊙B相交于C、D两点，则弦CD长的所有可能的整数值有（）个。A.1B.2C.3D.4第2页共8页8.如图，PA、PB、CD分别与圆O相切于A、B、E,若∠COD=500,则∠P=（）A.80°B.55°C.130°D.65°第8题图第9题图第10题图9.如图,在平面直角坐标系中，四边形OABC为正方形，顶点A，C在坐标轴上，以边AB为弦的⊙M与x轴相切，若点A的坐标为(0,8)，则圆心M的坐标为()A.(4,5)B.(-5,4)C.(-4,6)D.(-4,5)10.如图,半圆O与等腰直角三角形两腰CA，CB分别切于D，E两点，直径FG在AB上，若BG=1-2，则△ABC的周长为()A.4＋22B.6C.2＋22D.411.如图,△ABC内接于⊙O，其外角平分线AD交⊙O于DM⊥AC于M，下列结论：①DB=DC；②AC-AB=2AM；③AC+AB=2CM；④CDBABDSS2.其中正确的有()A.只有④②B.只有①②③C.只有③④D.①②③④12.如图，⊙O上有两定点A与B，若动点P点从点B出发在圆上匀速运动一周，那么弦AP的长度d与时间t的关系可能是下列图形中的（）A.①或④B.①或③C.②或③D.②或④第3页共8页二填空题:13.如图,⊙O的半径为5,P为圆内一点,P到圆心O的距离为4,则过P点的弦长的最小值是．第13题图第14题图第15题图14.如图,⊙O是四边形ABCD的内切圆,E、F、G、H是切点,点P是优弧EFH上异于E、H的点,若∠A=500,则∠EPH=．15.如图，AB与⊙O相切于点B，AO的连线交⊙O于点C,若∠A=500,则∠ABC为.16.如图，PA、PB切⊙O于点A、B，点C是⊙O上一点，且∠ACB=650,则∠P=度．第16题图第17题图第18题图17.如图，点A、B、C在⊙O上，∠AOC=600,则∠ABC的度数是．18.等腰△ABC的顶角∠A=1200,腰AB=AC=10,△ABC的外接圆半径等于.19.△ABC中，AB=5，BC=8，∠ABC=600，则△ABC的内切圆半径为__________．20.直线343xy与x轴、y轴分别交于A、B两点,已知点C(0,-1)、D(0,k)，以点D为圆心、DC为半径作⊙D,当⊙D与直线AB相切时,k的值为．21.如图，⊙P内含于⊙O，⊙O的弦AB切⊙P于点C，且AB∥OP．若阴影部分的面积为10π，则弦AB的长为.第21题图第22题图22.如图，圆心O恰好为正方形ABCD的中心，已知AB=4，⊙O的直径为1，现将⊙O沿某一方向平移，当它与正方形ABCD的某条边相切时停止平移，记平移的距离为d，则d的取值范围是≤d≤.第4页共8页三简答题:23.如图，已知AB是⊙O的直径，BC是和⊙O相切于点B的切线，⊙O的弦AD平行于OC．求证：DC是⊙O的切线.24.如图,已知直线AC与圆O交于B、C,直线AD过圆心O,若圆O的半径是5,且∠DAC=300,AD=13,求弦BC长.25.如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE，过C作CD⊥PA,垂足为D.（1）求证：CD为⊙O的切线；（2）若DC+DA=6，⊙O的直径为10，求AB的长度．第5页共8页26.如图1,AB是圆O的直径,点C在AB的延长线上,AB=4,BC=2,P是圆O上半部分的一个动点,连接OP,CP．（1）求△OPC的最大面积；（2）求∠OCP的最大度数;设∠OCP=ɑ,当线段CP与圆O只有一个公共点(即P点)时，求ɑ的范围(直接写出答案)；（3）如图2,延长PO交圆O于点D,连接DB,当CP=DB.求证:CP是圆O的切线．27.如图,在Rt△ABC中,...