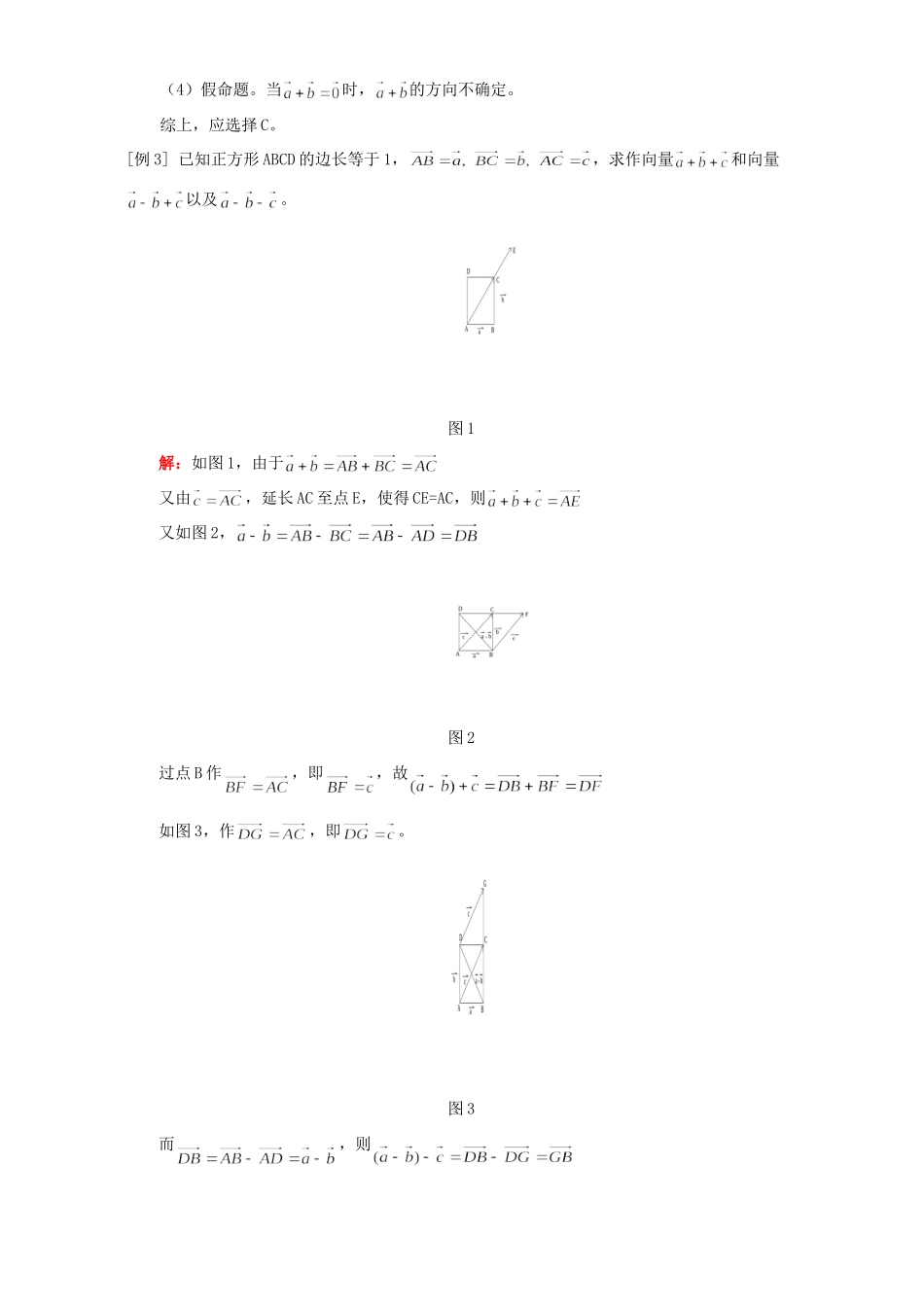
向量、向量的加法与减法例题解析一.本周教学内容:向量、向量的加法与减法二.重点、难点:1.向量的概念。2.向量的加法与减法的定义。3.会用加法与减法的平行四边形法则和三角形法则作出向量的和与差。【典型例题】[例1]以下命题中真命题的个数是()(1)(2)(3)(4)向量与向量平行,则、的方向相同或相反。A.0B.1C.2D.3解:(1)假命题。因为两向量之差仍为向量,所以应。(2)假命题。因为实数与向量的积是向量,所以应有。(3)真命题。。(4)假命题。若与中有一个为,则它的方向不确定。综上,应选择B。[例2]下列命题中假命题的个数是()(1)向量与是共线向量,则A、B、C、D四点共线。(2)四边形ABCD是平行四边形的充要条件是。(3)四边形ABCD中,。(4)若两非零向量,与的方向相同或相反,则的方向必与或的方向相同。A.1B.2C.3D.4解:(1)是假命题。共线向量是指平行向量,故与平行不一定A、B、C、D四点共线。(2)真命题。(3)假命题,由ABCD为四边形,则有,故。(4)假命题。当时,的方向不确定。综上,应选择C。[例3]已知正方形ABCD的边长等于1,,求作向量和向量以及。图1解:如图1,由于又由,延长AC至点E,使得CE=AC,则又如图2,图2过点B作,即,故如图3,作,即。图3而,则[例4]设P是的重心,试证明:。证明:如图设M、N、P分别是边BC、AC、AB的中点,由,则有又由M是BC中点,故,即同理可得,故又由点P是的重心则,故又由,则故[例5]试比较下列向量模的大小(1)与;(2)与。解:(1)分情况讨论①当、中至少有一个为时,=;②当、均为非零向量时,若与同向,则=若与异向,则<若与不共线,则<(2)①当与中至少有一个为时,则②当与均为非零向量时,根据向量加减法的平行四边形法则可知,与是以、为边的平行四边形的两条对角线的长,如图分三种情况讨论,设与的夹角为。图1图2图3若,如图1,则有若,如图2,则有若,如图3,则有[例6]设点G为四边形ABCD对角线的中点连线MN的中点,点P为该平面内任意一点,证明。证明:如图所示,设四边形ABCD的对角线AC、BD中点分别为M、N由PM为的中线,故同理可知又由G为MN中点,则有即特别地,当P与G重合时可以得到一.选择题:1.下列命题中正确的个数为()(1)若向量与共线,与共线,则向量与共线(2)共线的单位向量都相等(3)向量与反向,,则向量与的方向相同(4)向量与不共线,则、均为非零向量A.1个B.2个C.3个D.4个2.平行四边形ABCD中,等于()A.B.C.D.3.非零向量、不共线,且,则向量+与-的关系是()A.平行B.垂直C.相交但不垂直D.相等4.已知的三个顶点A、B、C及平面内一点P,若,则点P与的位置关系是()A.P在内部B.P在外部C.P在AB边上或它的延长线上D.P在AC边上且为AC的一个三等分点二.填空题5.已知AD、BE分别是的边BC、AC上的中线,且,则。6.点P为四边形ABCD内部一点,,,点E、F分别为AB、CD的中点,则。三.证明题:7.任意四边形ABCD的边AD、BC的中点分别为E、F,求证:。8.用向量方法证明:四边形为平行四边形的充要条件是它的两条对角线互相平分。[参考答案]一.1.B(析:(1)与(4)正确)2.D3.B4.D二.5.6.三.7.证法一:如图,则同理,由,则故由E、F分别为AD、BC中点,则,故证法二:如图,在平面内取点O,作、,则有又由证法三:如图,作,则四边形ABGC为平行四边形,故对角线AG过BC中点F,则EF为的中位线,故,又由,所以8.证明:先证充分性,若四边形对角线互相平分,如图则有,故,则四边形ABCD为平行四边形再证必要性,设AC中点为O1,BD中点O2,在平行四边形ABCD中故,则,由于,因此有又由加法法则,,故故O1与O2重合