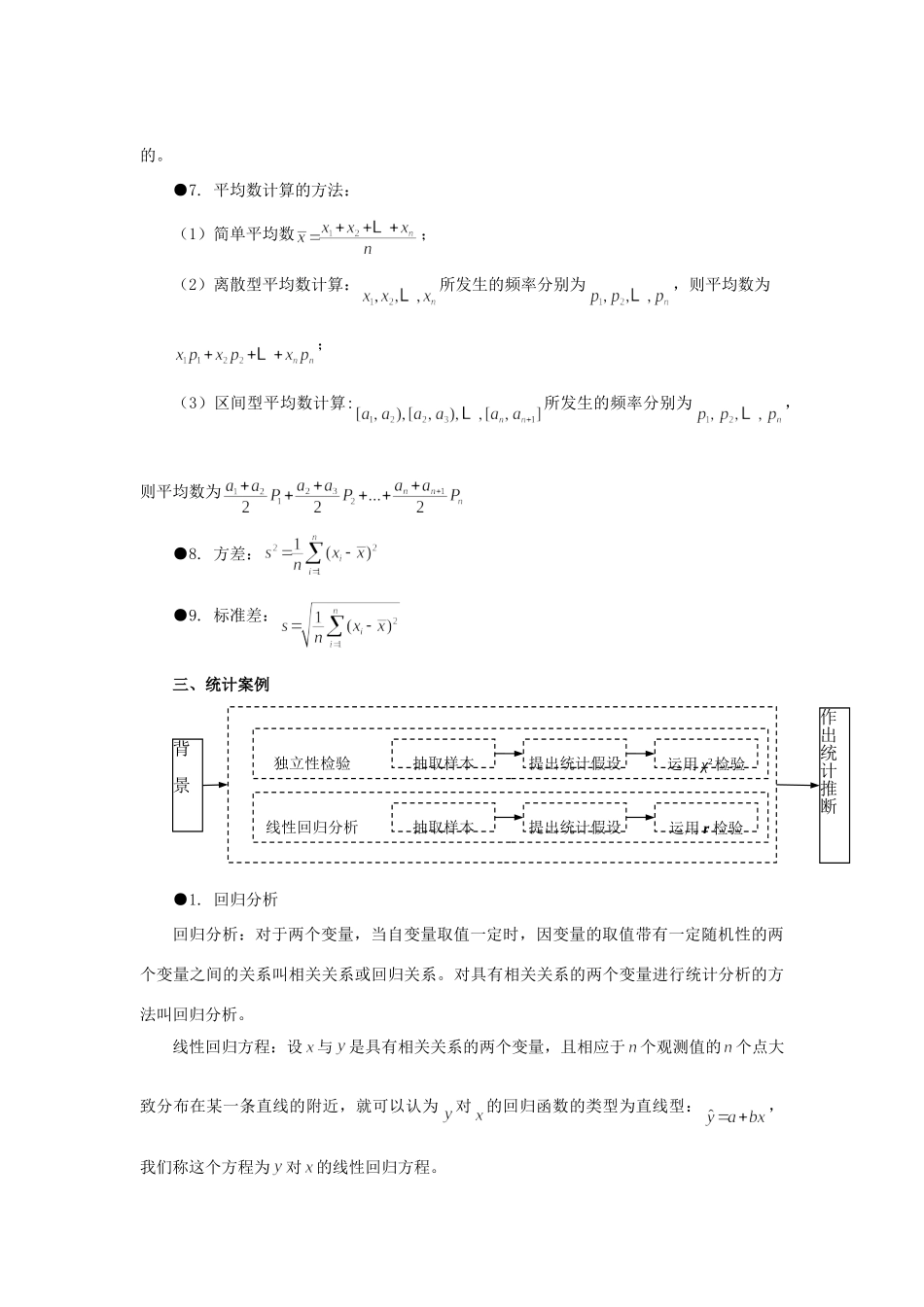
专题八之统计【知识概要】一、抽样方法●1.简单随机抽样——设一个总体的总数为N,若通过逐个抽取的方法从总体中抽取一个样本,且每次抽取时,各个个体被抽到的概率相等,这样的抽样方法叫简单随机抽样。特点:不放回抽样;逐个抽取;被抽取的样本的总数是有限的。主要方法:抽签法;随机数表法。●2.系统抽样——将总体平均分成几个部分,然后按照预先定出的规则,从每个部分中抽取一个个体,得到所需的样本,这样的抽样方法叫简单系统抽样。特点:等概率抽样;等距离(或按预先定出的规则)抽样;不放回抽样。系统抽样的步骤:①采用随机的方式将总体中的个体编号;②将整个的编号按一定的间隔(设为k),当(N为总体中的个体数,n为样本容量)是整数时,当不是整数时,从总体中剔除一些个体,使剩下的总体中个体的个数能被n整除,这时,并将剩下的总体重新编号;③在第一段中用简单随机抽样确定起始的个体标号l;④将编号为的个体抽出。●3.分层抽样——当总体由差异明显的几个部分组成时,将总体中的个体按不同的特点分成层次比较分明的几部分,然后按各部分在总体中所占的比进行抽样,这样的抽样方法叫分层抽样。特点:每层抽取的样本数=;等概率抽样;不放回抽样。分层抽样的步骤:①将总体按一定标准分层;②计算各层的个数与总体的个数的比;③按各层个数占总体的个数的比确定各层应抽取的样本容量;④在每一层进行抽样(可用简单随机抽样或系统抽样)。二、总体分布的估计和总体特征数的估计●1.频率分布表的有关概念(1)频数:在一组数据中,某范围内的数据出现的次数;(2)频率:频数除以数据的总个数;(3)全距:数据中最大与最小值的差;(4)组距=;(5)分组要求:通常对组内数值所在区间取左开右闭区间,最后一组取闭区间,并且使分点比数据多一位小数。●2.频率分布直方图具体做法如下:(1)求极差(即一组数据中最大值与最小值的差);(2)决定组距与组数;(3)将数据分组;(4)列频率分布表;(5)画频率分布直方图:①横轴表示样本数据,纵轴表示频率与组距的比值;②以每个组距为底,以各频率除以组距的商为高,分别画成矩形;③图中每个矩形的面积等于相应组的频率,即:;④各组频率的和等于1,即各小矩形的面积的和等于1。●3.频率分布折线图:将频率分布直方图中,取各相邻矩形的上底边中点顺次连接,再将矩形的边去掉,就得到频率分布折线图。●4.密度曲线:当样本容量取得足够大,分组的组距取得足够小,则这条折线就越接近于一条光滑的曲线,这条光滑的曲线称为总体密度曲线。●5.中位数:将数据按从小到大或从大到小排列,处在中间位置上的一个数据(或中间两位数据的平均数)叫做这组数据的中位数。●6.众数:在一组数据中出现次数最多的数叫做这组数据的众数;众数不一定是唯一的。●7.平均数计算的方法:(1)简单平均数;(2)离散型平均数计算:所发生的频率分别为,则平均数为;(3)区间型平均数计算:所发生的频率分别为,则平均数为●8.方差:●9.标准差:三、统计案例●1.回归分析回归分析:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫相关关系或回归关系。对具有相关关系的两个变量进行统计分析的方法叫回归分析。线性回归方程:设与是具有相关关系的两个变量,且相应于个观测值的个点大致分布在某一条直线的附近,就可以认为对的回归函数的类型为直线型:,我们称这个方程为对的线性回归方程。背景独立性检验线性回归分析抽取样本抽取样本提出统计假设提出统计假设运用χ2检验运用r检验作出统计推断(1)设两个具有线性相关的一组数据为:则线性回归方程为:其中,分别为,的算术平均数。(2)特点:线性回归方程过点;●2.相关系数对于变量y与x的一组观测值,把叫做变量y与x之间的样本相关系数,简称相关系数,用它衡量两个变量之间的线性相关程度。相关系数的性质:≤1,且越接近1,相关程度越大;越接近0,相关程度越小。●3独立性检验独立性检验是对两种分类变量之间是否有关系进行检验。①独立性检验的必要性:2×2列联表中的数据是样本数据,它只是总体的代表,具有随机性,故需要用列联...