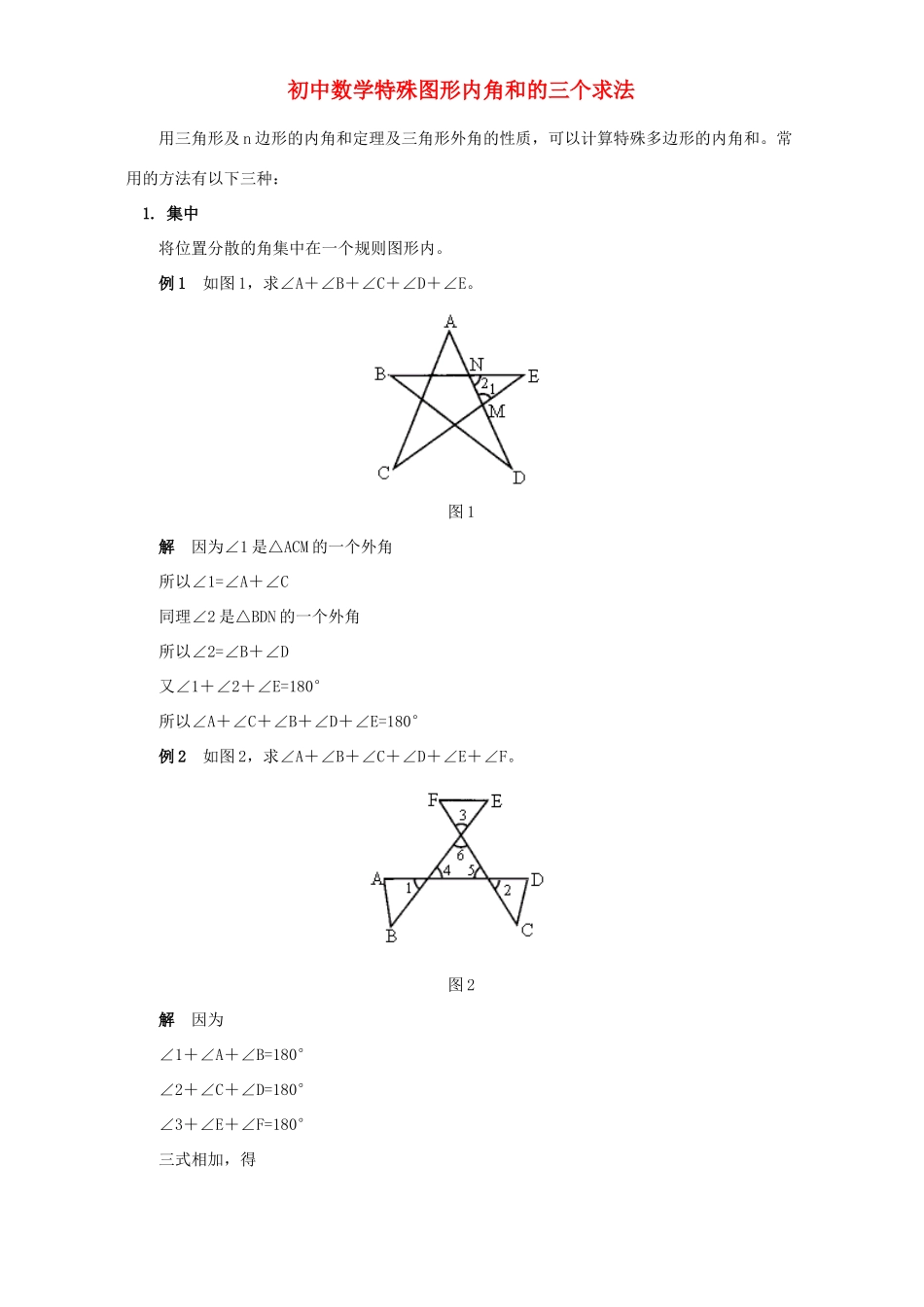
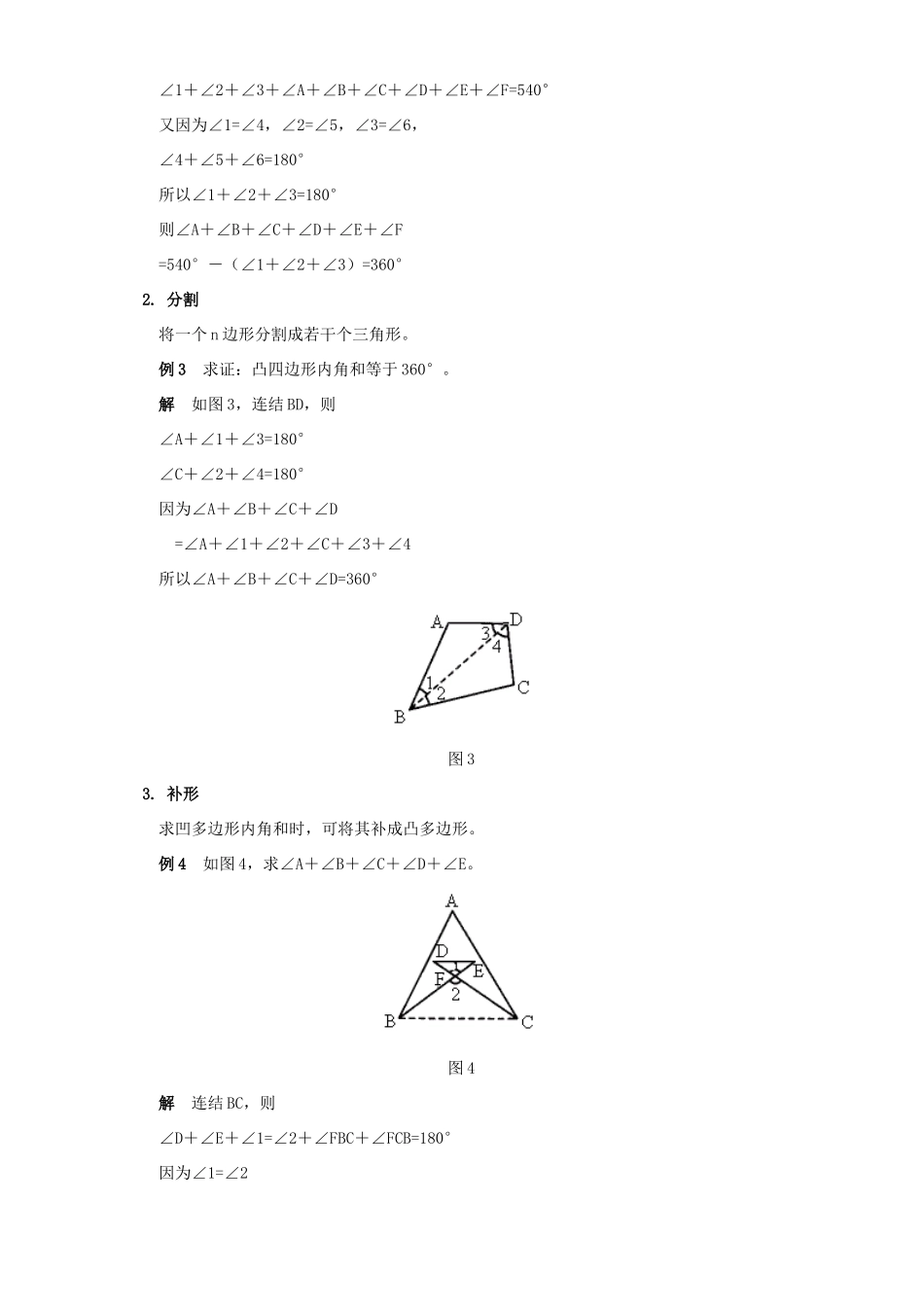
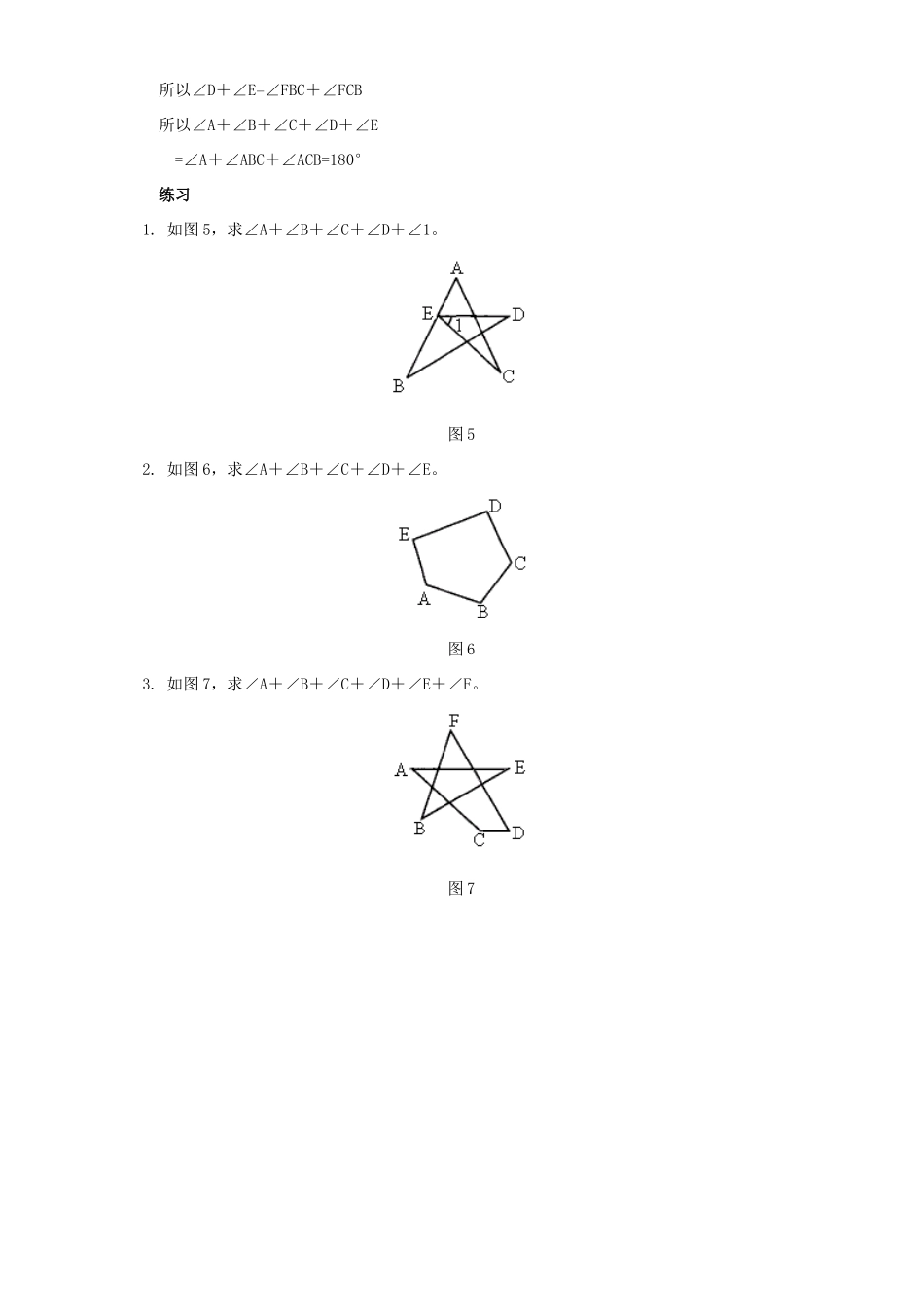
初中数学特殊图形内角和的三个求法用三角形及n边形的内角和定理及三角形外角的性质,可以计算特殊多边形的内角和。常用的方法有以下三种:1.集中将位置分散的角集中在一个规则图形内。例1如图1,求∠A+∠B+∠C+∠D+∠E。图1解因为∠1是△ACM的一个外角所以∠1=∠A+∠C同理∠2是△BDN的一个外角所以∠2=∠B+∠D又∠1+∠2+∠E=180°所以∠A+∠C+∠B+∠D+∠E=180°例2如图2,求∠A+∠B+∠C+∠D+∠E+∠F。图2解因为∠1+∠A+∠B=180°∠2+∠C+∠D=180°∠3+∠E+∠F=180°三式相加,得∠1+∠2+∠3+∠A+∠B+∠C+∠D+∠E+∠F=540°又因为∠1=∠4,∠2=∠5,∠3=∠6,∠4+∠5+∠6=180°所以∠1+∠2+∠3=180°则∠A+∠B+∠C+∠D+∠E+∠F=540°-(∠1+∠2+∠3)=360°2.分割将一个n边形分割成若干个三角形。例3求证:凸四边形内角和等于360°。解如图3,连结BD,则∠A+∠1+∠3=180°∠C+∠2+∠4=180°因为∠A+∠B+∠C+∠D=∠A+∠1+∠2+∠C+∠3+∠4所以∠A+∠B+∠C+∠D=360°图33.补形求凹多边形内角和时,可将其补成凸多边形。例4如图4,求∠A+∠B+∠C+∠D+∠E。图4解连结BC,则∠D+∠E+∠1=∠2+∠FBC+∠FCB=180°因为∠1=∠2所以∠D+∠E=∠FBC+∠FCB所以∠A+∠B+∠C+∠D+∠E=∠A+∠ABC+∠ACB=180°练习1.如图5,求∠A+∠B+∠C+∠D+∠1。图52.如图6,求∠A+∠B+∠C+∠D+∠E。图63.如图7,求∠A+∠B+∠C+∠D+∠E+∠F。图7