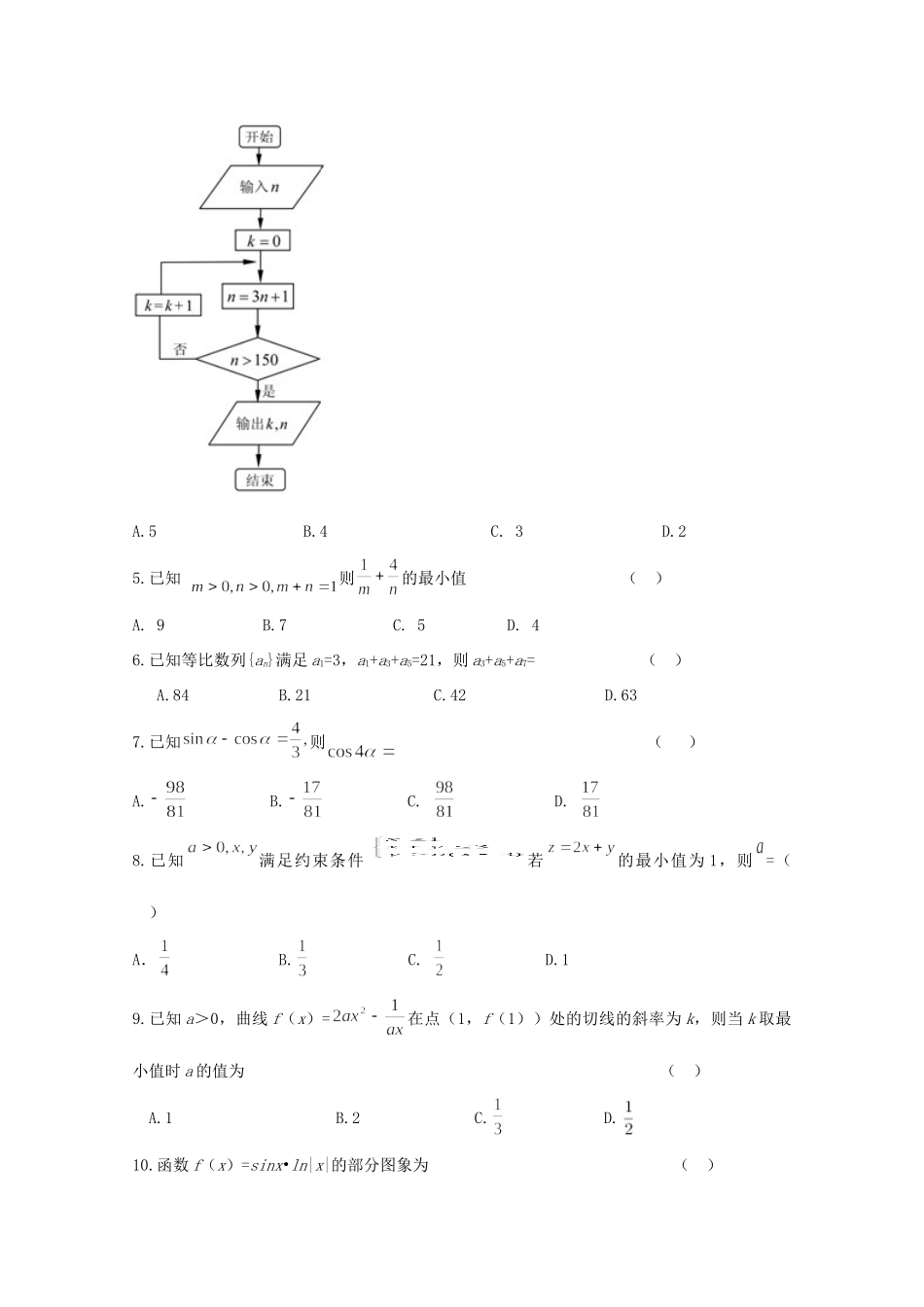
2017-2018学年第一学期高三年级统练二数学(文科)试题一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x2-3x+2<0},B={x|y=lg(3-x)},则A∩B=()A.{x|x<3}B.{x|1<x<3}C.{x|2<x<3}D.{x|1<x<2}2.已知复数的实部与虚部相等,其中为实数,则=()A.B.C.2D.33.“”是“”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.阅读如图的程序框图.若输入n=5,则输出k的值为()A.5B.4C.3D.25.已知则的最小值()A.9B.7C.5D.46.已知等比数列{an}满足a1=3,a1+a3+a5=21,则a3+a5+a7=()A.84B.21C.42D.637.已知则()A.B.C.D.8.已知满足约束条件若的最小值为1,则=()A.B.C.D.19.已知a>0,曲线f(x)=在点(1,f(1))处的切线的斜率为k,则当k取最小值时a的值为()A.1B.2C.D.10.函数f(x)=sinx•ln|x|的部分图象为()A.B.C.D.11.已知函数y=f(x),对任意自变量x都有f(x)=f(2-x),且函数f(x)在[1,+∞)上单调.若数列{an}是公差不为0的等差数列,且f(a6)=f(a2012),则{an}的前2017项之和为()A.2017B.2018C.0D.112.已知函数f(x)=,若数列{an}满足an=f(n)(n∈N﹡),且{an}是递增数列,则实数a的取值范围是()A.B.C.(2,3)D.(1,3)二、填空题:(本大题共4小题,每小题5分,共20分)13.已知向量=(1,2),=(x,-1),若,则=______.14.设实数x,y满足,则z=2x+y的最小值______.15.在△ABC中,A、B、C的对边分别为a、b、c,且bcosC=3acosB-ccosB,,则△ABC的面积为______16.定义在R上的可导函数f(x)的导函数为,满足<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为______.三、解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。)17.(12分)已知函数的最小正周期为π.(1)求的值;(2)求f(x)的单调递增区间.18.(12分)已知{an}为等差数列,且a1+a3=8,a2+a4=12.(1)求{an}的通项公式(2)记{an}的前n项和为Sn,若a1,ak,Sk+2成等比数列,求正整数k的值.19.(12分)已知向量=(sinx,-1),=(cosx,3).(1)当∥时,求的值;(2)已知在锐角△ABC中,a,b,c分别为角A,B,C的对边,=2asin(A+B),函数f(x)=,求f(B+)的取值范围.20.(12分)已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项.(1)求数列{an}的通项公式;,Sn=b1+b2+b3+…+bn,对任意正整数n,Sn+(n+m)an+1<0恒成立,试求m的取值范围.21.(12分)已知f(x)=.(1)求f(x)的最大值;(2)令g(x)=ax2-2lnx,当x>0时,f(x)的最大值为M,g(x)=M有两个不同的根,求a的取值范围;(3)存在x1,x2∈(1,+∞),且x1≠x2,使得|f(x1)-f(x2)|≥k|lnx1-lnx2|成立,求k的取值范围.22.(10分)设函数f(x)=|x+2|-|x-1|.(1)求不等式f(x)>1解集;(2)若关于x的不等式f(x)+4≥|1-2m|有解,求实数m的取值范围.