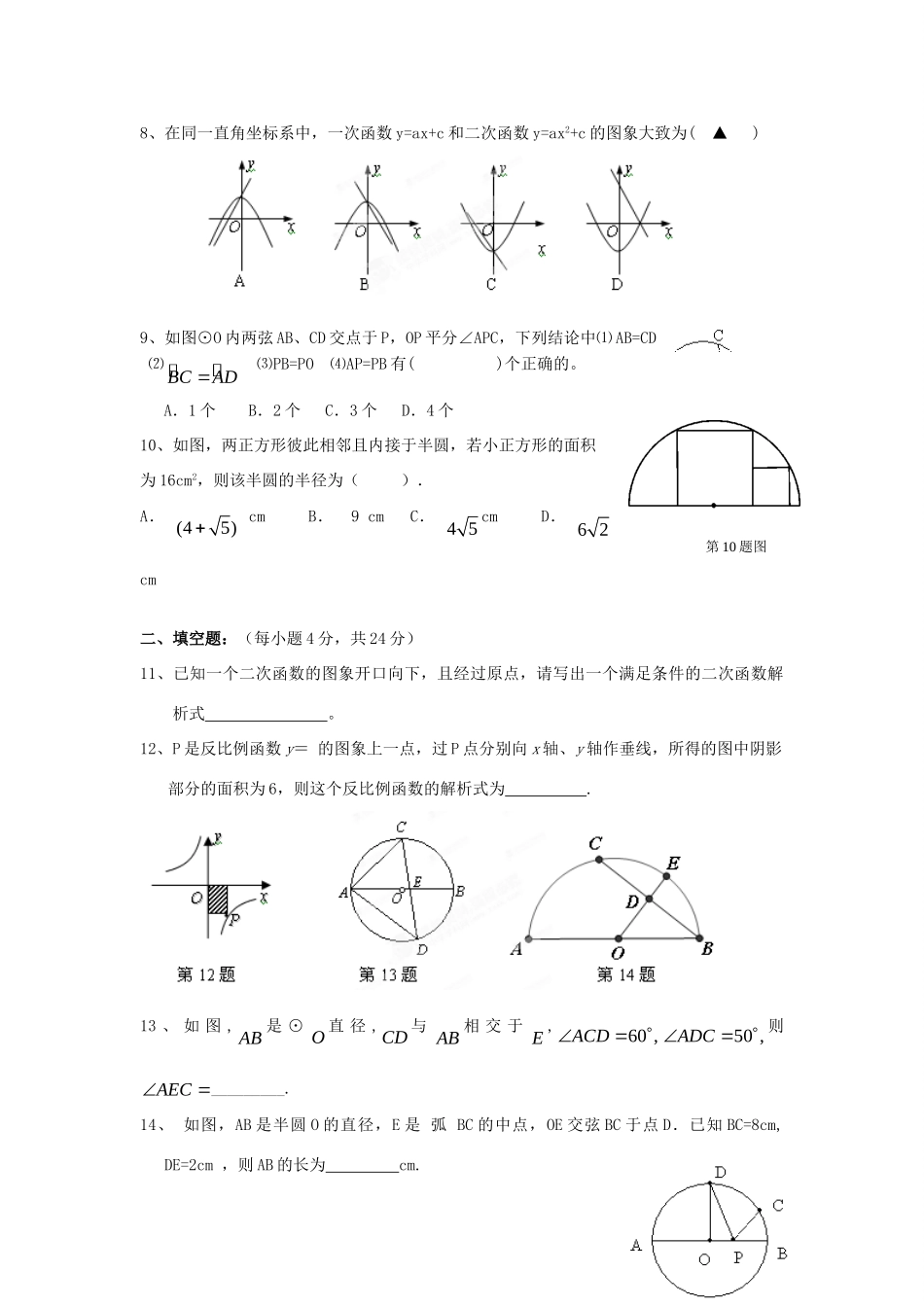
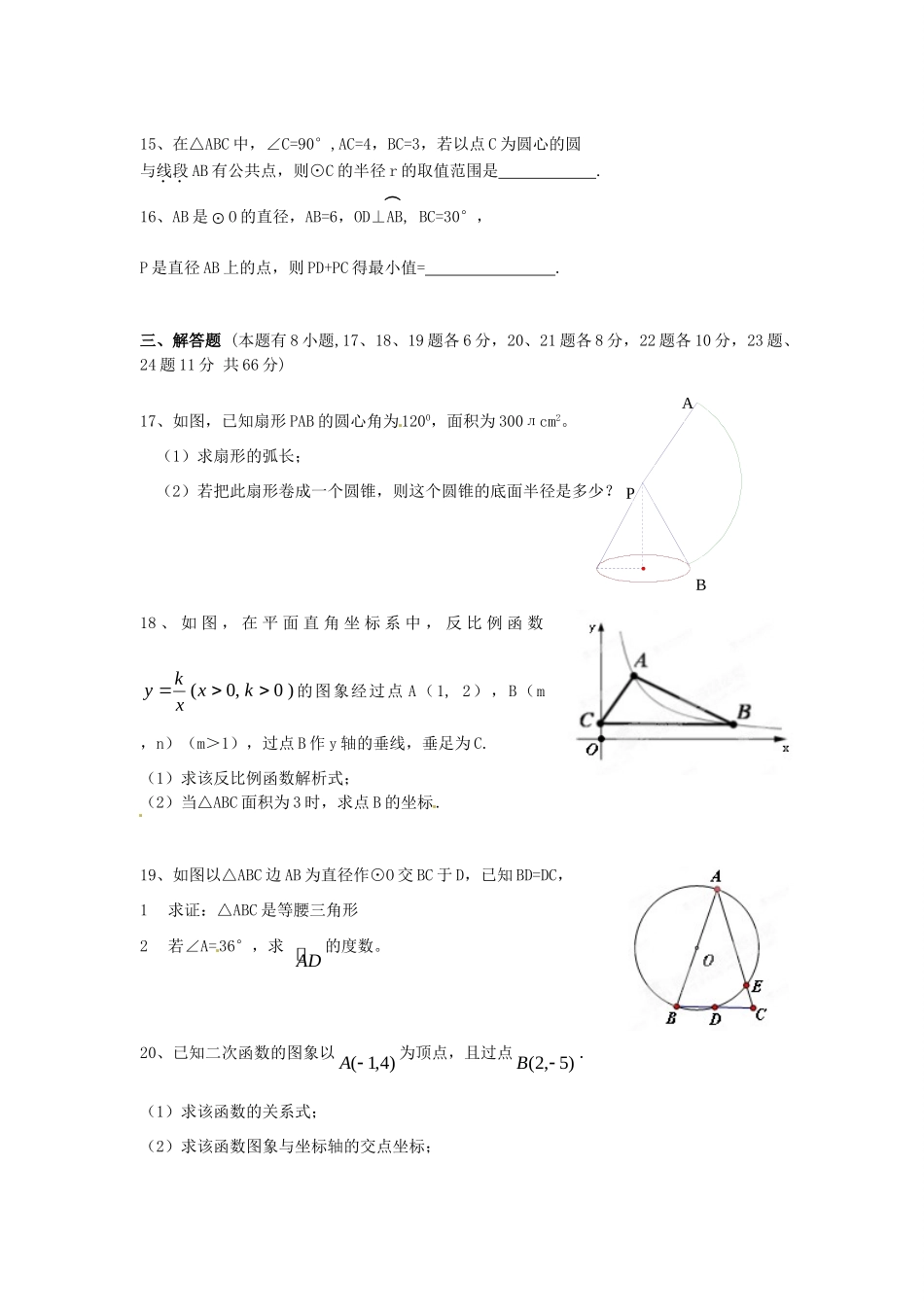
浙江省乐清市育英寄宿学校2014届九年级9月月考数学(普通班)试题(无答案)浙教版一、选择题(本题有10小题,每小题3分,共30分.)1、二次函数y=(x-1)2+2,它的图像顶点坐标是(▲)A.(-2,1)B.(2,1)C.(2,-1)D.(1,2)2、已知点M(-2,3)在双曲线xky上,则下列各点一定在该双曲线上的是(▲)。A、(3,-2)B、(-2,-3)C、(2,3)D、(3,2)3、⊙O的半径为4,如图圆心O的坐标为)0,0(,点A的坐标为)2,4(,则点A与⊙O的位置关系是(▲)A.点A在⊙O内B.点A在⊙O外C.点A在⊙O上D.不能确定4、在RT△ABC中,AB=12,BC=16,那么这个三角形的外接圆的直径是(▲).A.10B.20C.10或8D.20或165、如图,O是线段BC的中点,A、D、C到O点的距离相等。若30ABC,则ADC的度数是(▲)A.30°B.60°C.120°D.150°6.二次函数cbxaxy2的图象如图所示,则下列关系式不正确的是(▲)A.a<0B.abc>0C.cba>0D.acb42>07、已知一个扇形的弧长为10πcm,圆心角是150º,则它的半径长为(▲)A.12cmB.10cmC.8cmD.6cm8、在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为(▲)9、如图⊙O内两弦AB、CD交点于P,OP平分∠APC,下列结论中⑴AB=CD⑵BCAD⑶PB=PO⑷AP=PB有()个正确的。A.1个B.2个C.3个D.4个10、如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为().A.(45)cmB.9cmC.45cmD.62cm二、填空题:(每小题4分,共24分)11、已知一个二次函数的图象开口向下,且经过原点,请写出一个满足条件的二次函数解析式。12、P是反比例函数y=的图象上一点,过P点分别向x轴、y轴作垂线,所得的图中阴影部分的面积为6,则这个反比例函数的解析式为.13、如图,AB是⊙O直径,CD与AB相交于E,60,ACD50,ADC则AEC_________.14、如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D.已知BC=8cm,DE=2cm,则AB的长为cm.第10题图15、在△ABC中,∠C=90°,AC=4,BC=3,若以点C为圆心的圆与线段AB有公共点,则⊙C的半径r的取值范围是.︵16、AB是O的直径,AB=6,OD⊥AB,BC=30°,P是直径AB上的点,则PD+PC得最小值=.三、解答题(本题有8小题,17、18、19题各6分,20、21题各8分,22题各10分,23题、24题11分共66分)17、如图,已知扇形PAB的圆心角为1200,面积为300лcm2。(1)求扇形的弧长;(2)若把此扇形卷成一个圆锥,则这个圆锥的底面半径是多少?18、如图,在平面直角坐标系中,反比例函数)0,0(kxxky的图象经过点A(1,2),B(m,n)(m>1),过点B作y轴的垂线,垂足为C.(1)求该反比例函数解析式;(2)当△ABC面积为3时,求点B的坐标.19、如图以△ABC边AB为直径作⊙O交BC于D,已知BD=DC,1求证:△ABC是等腰三角形2若∠A=36°,求AD的度数。20、已知二次函数的图象以)4,1(A为顶点,且过点)5,2(B.(1)求该函数的关系式;(2)求该函数图象与坐标轴的交点坐标;PAB(3)当函数值大于0时,自变量的取值范围是什么?21、如图,在⊙M中,弦AB所对的圆心角为120度,已知圆的半径为2cm,并建立如图所示的直角坐标系。(1)求圆心M的坐标;(2)设点P是⊙M上的一个动点,当PABRtPAB为时,求点P的坐标。22、有一座抛物线型拱桥,桥下面在正常水位AB时宽20m.水位上升3m,就达到警戒线CD,这时,水面宽度为10m.(1)在如图所示的坐标系中求抛物线的表达式;(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?23、在直角坐标平面中,O为坐标原点,二次函数y=-x2-(k-1)x+2的图像与y轴交与点A,与x轴的负半轴交于点B,且S△OAB=3.(1)求点A与点B的坐标;(2)求此二次函数的解析式;(3)如果点P在x轴上,且△ABP是等腰三角形,请直接写出P点的坐标.24、如图。以点P(1,-2)为圆心,22为半径的⊙P交X轴于点A,B抛物线2yaxbxc经过点A,B和点M(1,-8).(1)求点A,B坐标(2)求抛物线的解析式(3)抛物线上是否存在点Q,使PQ和OM互相平分。如果存在,求出点Q坐标。不存在请简要说明理由。