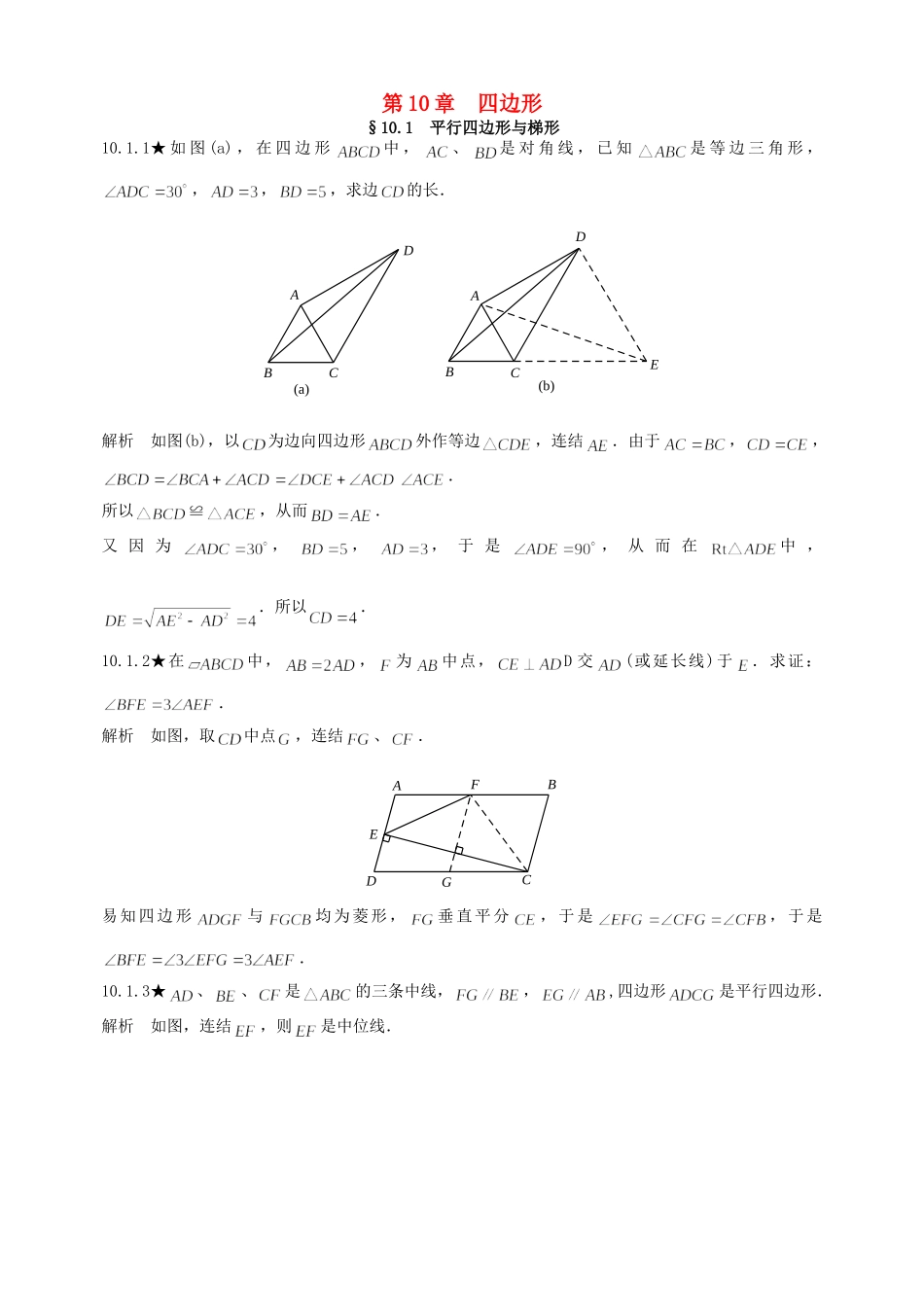
第10章四边形§10.1平行四边形与梯形10.1.1★如图(a),在四边形中,、是对角线,已知是等边三角形,,,,求边的长.DABCDABCE(a)(b)解析如图(b),以为边向四边形外作等边,连结.由于,,.所以≌,从而.又因为,,,于是,从而在中,.所以.10.1.2★在中,,为中点,D交(或延长线)于.求证:.解析如图,取中点,连结、.AFBEDGC易知四边形与均为菱形,垂直平分,于是,于是.10.1.3★、、是的三条中线,,,四边形是平行四边形.解析如图,连结,则是中位线.AGFEBDC由条件知,故,于是,故结论成立.10.1.4★延长矩形的边到,使,是的中点,求证:.解析如图,取中点,连结,则,于是.ADBCADFGEBC题10.1.4题10.1.510.1.5★菱形中,,,求菱形的面积.解析如图,易知与均为正三角形.设菱形边长为,则由,得,,所以,,因此菱形面积为.10.1.6★在梯形中,,中位线分别交、、、于、、、,若延长、的交点正好位于上,求.ADMQPNBRC解析设、延长后交于,且在上,则由中位线知,,,故.10.1.7★★四边形中,,,,,,求.解析如图所示,作,分别交所在直线于、,作交于,则为等腰直角三角形,,,故;,,,故,.FBCEADG所以,.从而.10.1.8★★★已知中,,是上一点,关于、的对称点分别为、,若,.解析如图,连结、、、.FAEBDC由对称,有,故、、共线.又,故,而,所以梯为等腰梯形.又,于是.10.1.9★★将梯形的各个顶点均作关于不包含该顶点的对角线的对称点,证明:如果所得到的四个像点也形成四边形,则必为一个梯形.B'C'ADBCA'D'O解析如图,,、、、关于对应对角线的对称点分别为′、′、′、′.设、交于,连结′、′、′、′.则′=′,故′、、′共线,且,同理′、、′共线,,所以由得.故如′、′、′、′不位于同一直线上,则′′′′,即′′′′成梯形.10.1.10★已知:直角梯形,,,,是上一点,,,求.ADEBC解析如图,连结,则由,,得.又,故≌,.又,故为正三角形,于是.10.1.11★★在四边形中,,,,,求、和的长.ABCED解析如图,延长、至,则,.又,故,,又,,故.至于求,有多种方法,如勾股定理或余弦定理,也可用、、、四点共圆的性质:,.§10.2正方形10.2.1★在正方形中,为的中点,为上的点,且.求证:.ADBECFP解析如图,延长、,设交于,则得,.于是,即.10.2.2★正方形边长等于1,通过它的中心引一条直线,求正方形的四个顶点到这条直线的距离平方和的取值范围.AMDONBCl解析如图,设是正方形的中心,通过,、分别与垂直于、.由于,,故≌,.对、的垂线也有类似结论,因此所求距离的平方和是常数1.10.2.3★正方形的对角线交于,的平分线交于,交于,求证:.解析如图,作,交于,为中位线,.问题变为证明.因为么,于是结论成立.ADEOGBFC10.2.4★设、分别为正方形的边、的中点,且与交于,求证:.解析如图,由知≌,故,故.延长、,设交于,则,为直角三角形斜边之中点,于是.QADMBCNP题10.2.410.2.5★已知两个正方形、(顶点均按照顺时针方向排列),求证:这两个正方形的中心和、的中点组成一个正方形.题10.2.5MAQBPCDRSLK解析如图,设、、、的中点分别为、、、.由于,,,于是≌,由此得与垂直且相等.由于,,故四边形为正方形.10.2.6★★是正方形内一点,若,,求.解析如图,作于,则ADBLCMN解得,.不妨设,,,则,,由条件,知,即,解得.又作于,于是,,故.10.2.7★是正方形的两对角线的交点,是上异于的任一点,于,于,是的延长线和的交点,求.CGBOPFDEA解析如图,易知,,,于是≌≌,于是,,故为等腰直角三角形,.10.2.8★★是正方形的边的中点,点分对角线的比为,证明:.解析连结,由正方形关于对称,知.又作于,由,易知,故为中点,垂直平分,于是,,或,故.AEDFPOBGC10.2.9★已知,向外作正方形和.直线垂直于,反向延长交于,求证:是的中点.解析如图,作、分别与直线垂直,垂足为、.PHMFQAEBKCG易见,,又,,故有≌,,同理,于是,.10.2.10★已知:正方形中,、分别在、上,于.若,求证:.反之,若,则.解析如图,延长至,使,连结,则≌,,,又,,故≌,、为其对应边上...