山东省济南市高三数学上学期9月质量检测试卷 理(PDF，无答案)试卷VIP免费

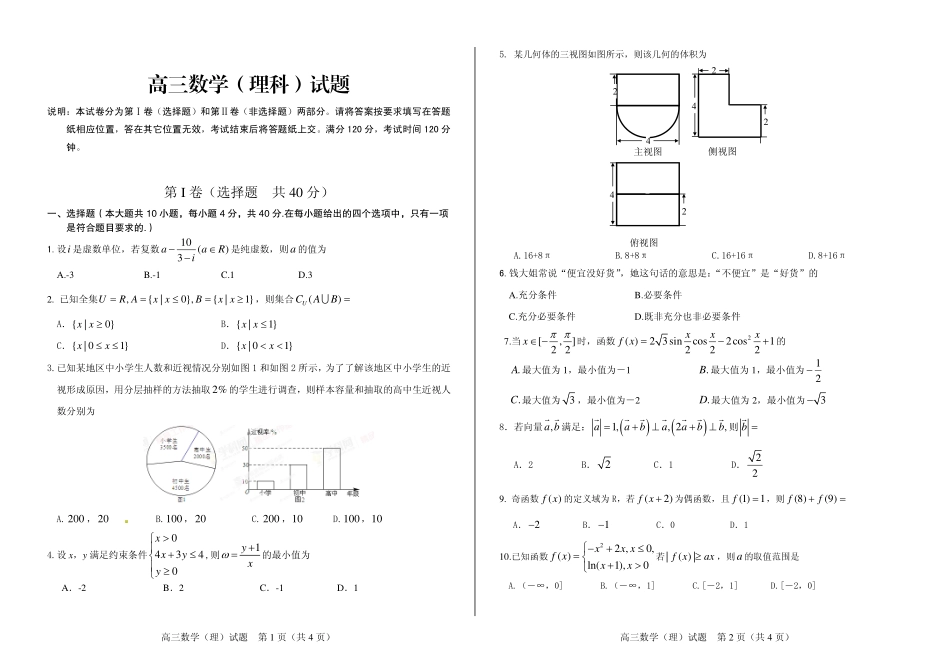
高三数学（理科）试题说明：本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。请将答案按要求填写在答题纸相应位置，答在其它位置无效，考试结束后将答题纸上交。满分120分，考试时间120分钟。第I卷（选择题共40分）一、选择题（本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.）1.设是虚数单位，若复数i10(3aia},B()UCAB0}B．{|1}xx)R是纯虚数，则的值为aA.-3B.-1C.1D.32.已知全集1}，则集合,{|0URAxx{|xxA．{|xx1}D．{|01}xxC．{|0xx3.已知某地区中小学生人数和近视情况分别如图1和如图2所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为，20A.200B.100，10D.100，4.设x，y满足约束条件04,则，20C.20010430xyyx1yx的最小值为A．-2B．2C．-1D．15.某几何体的三视图如图所示，则该几何的体积为A.16+8πB.8C.16+16πD.8+16π6.说“便宜没好货”句话的意思是：”是“好货”的+8π钱大姐常，她这“不便宜A.充分条件B.必要条件C.充分必要条件D.既非充分也非必要条件7.当[,]22x时，函数2(23sincos2c1222)osxxxfx的.A最大值为11.B最大值为1，最小值为，最小值为－21.C最大值为3，最小值为－2.D最大值为2，最小值为3,ab8．若向量满足：1,,2,aabaabb则bA．B．22C．1D．229.奇函数()fxR，若(2)fx的定义域为为偶函数，且(1)1f，则(8)(9)ffA．2B．1C．0D．1已知函数2()ln(1),0fxxx10.2,0,xxx若|()|fxax，则a的取值范围是A.（－∞，0]B.（－∞，1]C.[－2，1]D.[－2，0]侧视图2俯视图4442242主视图高三数学（理）试题第1页（共4页）高三数学（理）试题第2页（共4页）21.已知椭圆:E22221xyab（）的半焦距为，原点到经过两点，的0abcO,0c0,b19.某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为23和35.现安排甲组研发新产品A，乙组研发新产品B.设甲、乙两组的研发相互独立．（II）若新产品A研发成功，预计企业可获利润120万元；若新产品B研发成功，预计企业（III）若a＝1，求证：在区间[1，＋∞)上，函数f(x)的图象在函数g(x)＝23x3的图象的下方．第II卷（非选择题共80分）二、填空题（本大题共5小题，每小题4分，共20分）11.执行如图所示的程序框图，则输出的结果是.12．x＋12xn的展开式中第五项和第六项的二项式系数最大，则第四项为________．13.若*2sinsin...sin()777nnSnN，则在中，正数的个数是12100,...,SSS，.14.在△ABC中，B=60°,AB=2,BC=6,在BC上任取一点D,使△ABD为钝角三角形的概率为.15．已知点F是双曲线x2a2－y2b2＝1(a>0，b>0)的左焦点，点E是该双曲线的右顶点，过F且垂直于x轴的直线与双曲线交于A，B两点，若△ABE是锐角三角形，则该双曲线的离心率e的取值范围是.三、解答题：本大题共6小题，每小题10分，共60分.16.在△ABC中，内角A，B，C的对边,且，已知，,,abcac1cos3B，2BABC，，3b求：（Ⅰ）和的值；ac（Ⅱ）cosBC的值.17.如图，AB是圆的直径，垂直圆所在的平面，是圆上的点.PACPBCPAC（I）求证：平面平面；（II）若1，求证：二面角2ABACPA，1，CPBA的余弦值.18.设数列{an}的前n项和为Sn＝2n2，{bn}为等比数列，且a1＝b1，b2(a2－a1)＝b1.（I）求数列{an}和{bn}的通项公式；（II）设cn＝anbn，求数列{cn}的前n项和Tn.（I）求至少有一种新产品研发成功的概率；可获利润100万元．求该企业可获利润的分布列和数学期望．20.已知函数f(x)＝12x2＋alnx.（I）若a＝－1，求函数f(x)的极值，并指出是极大值还是极小值；（II）若a＝1，求函数f(x)在[1，e]上的最大值和最小值；直线的距离为12c．（Ⅰ）求椭圆E的离心率；（Ⅱ）如图，AB是圆:M225212xy的一条直径，若椭圆E经过,AB两点，高三数学（理）试题第3页（共4页）高三数学（理）试题第4页（共4页）求椭圆E的方程．