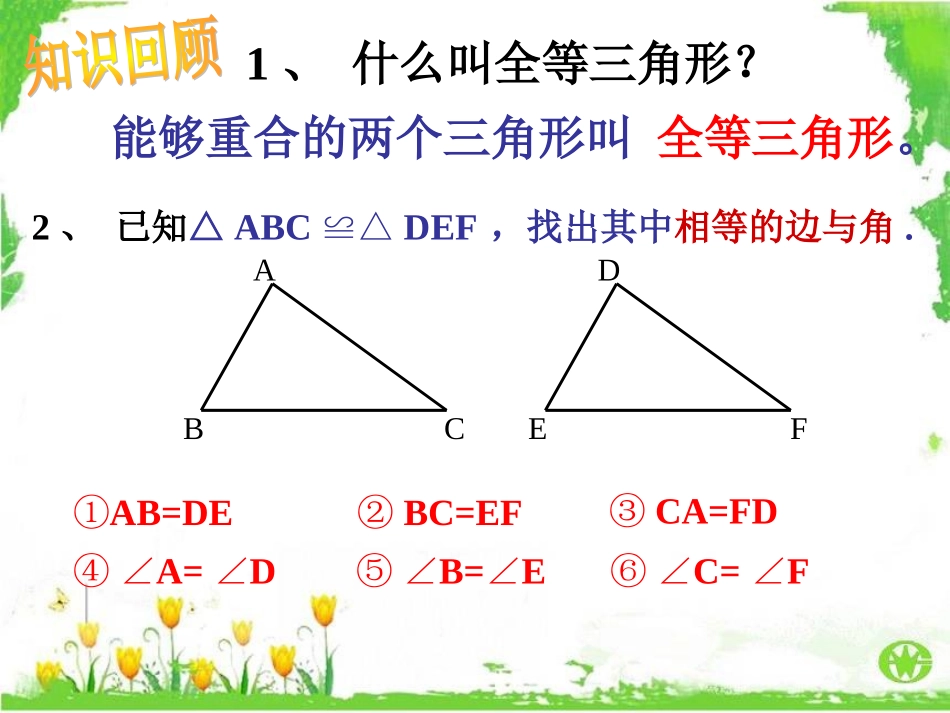
小测:小测:1.(2015重庆)已知一个多边形的内角和是900°,则这个多边形是边形。2.(2015滨州)在△ABC中,∠A:B:C=1:2:3∠∠,则∠C=。3.(2015菏泽)将一幅直角三角尺如图放置,若∠AOD=20°,则∠BOC的大小为。4.(2015柳州)如图,△ABCDEF≌△,则EF=。5.(2014淮安)如图,△ABDCBD≌△,若∠A=80°,∠ABC=70°,则∠ADC的度数为。第3题第4题第5题七七90°90°160°160°55130°130°1、什么叫全等三角形?能够重合的两个三角形叫全等三角形。2、已知△ABCDEF≌△,找出其中相等的边与角.ABCDEF①AB=DE②BC=EF③CA=FD④∠A=D∠⑤∠B=E∠⑥∠C=F∠ABCDEF①AB=DE③CA=FD②BC=EF④∠A=D∠⑤∠B=E∠⑥∠C=F∠1.满足这六个条件可以保证△ABCDEF≌△吗?2.如果只满足这些条件中的一部分,那么能保证△ABCDEF≌△吗?思考:思考:§12.2§12.2三角形全等的判定三角形全等的判定((一一))1、掌握边边边定理的内容。1、掌握边边边定理的内容。学习目标学习目标学习目标学习目标2、能初步应用边边边定理判定两个三角形全等。2、能初步应用边边边定理判定两个三角形全等。3、会作一个角等于已知角。3、会作一个角等于已知角。学习重点:学习重点:“边边边”定理。学习难点:学习难点:探索三角形全等的条件。4、通过探究三角形全等的条件的活动,培养自己合作交流的意识和大胆猜想、乐于探索的良好品质、以及发现问题的能力。4、通过探究三角形全等的条件的活动,培养自己合作交流的意识和大胆猜想、乐于探索的良好品质、以及发现问题的能力。1.1.只给一个条件只给一个条件..①①只给一条边:只给一条边:②②只给一个角:只给一个角:60°60°60°发现只给一个条件发现只给一个条件画出的三角形不能画出的三角形不能保证一定全等。保证一定全等。三角形全等的探究三角形全等的探究小组讨论:两个三角形全等一定需要6个条件吗?一个条件行吗?两个呢?2.2.给出两个条件:给出两个条件:①①一边一内角:一边一内角:②②两内角:两内角:③③两边:两边:30°30°30°30°30°50°50°2cm2cm4cm4cm发现给发现给出两个条件时画出出两个条件时画出的三角形也不能保的三角形也不能保证一定全等。证一定全等。三角形全等的探究三角形全等的探究如果给出三个条件画三角形,你能说出有哪几种可能的情况?②三边;③两边一角;④④两角一边。两角一边。①三角;已知两个三角形的三个内角分别30°,60°,90°,它们一定全等吗?这说明有三个角对应相等的两个三角形不一定全等。((11)三个角)三个角知识点一知识点一三角形全等的判定“三角形全等的判定“SSSSSS””探究探究22画任意一个△ABC,再画一个△A′B′C′,使A′B′=AB,B′C′=BC,A′C′=AC.这两个三角形全等吗?画图步骤参照:(1)画B′C′=BC;(3)连接线段A'B′、A′C′.(2)分别以点B′、C′为圆心,线段AB、AC长为半径画弧,两弧相交于点A′;ACBC′B′A′这个作图的这个作图的结果反映了结果反映了什么规律?什么规律?三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。ABCA’B’C’在△ABC和△A’B’C’中∴△ABCA’B’C’≌△(SSS)AB=A’B’BC=B’C’CA=C’A’用符号语言表达为:用符号语言表达为:三角形全等判定方法三角形全等判定方法11知识梳理:知识梳理:例已知:如图,AB=AD,BC=CD,求证:△ABCADC≌△ABCDACAC()≌AB=AD()BC=CD()∴△ABCADC△(SSS)证明:在△ABC和△ADC中=已知已知公共边ACBD分析:要证明两个三角形全等,需要那些条件?证明: D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABDACD≌△(SSS)例1如图,ABC△是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证:△ABDACD.≌△若要求证:若要求证:∠∠B=C∠B=C∠,,你会吗?你会吗?∴∠∠B=C(∠B=C(∠全等三角形的对应角相等全等三角形的对应角相等))1、如图,C是AB的中点,AD=CE,CD=BE。求证:△ACD≌△CBE∴AC=BC证明: C是AB的中点,∴在△ACD与△CBE中BECDCEADBCAC∴△ACD≌△CBE(SSS)ABCDE书本P37知识点二知识点二((尺规作图尺规作图))作一个角等于已知作...