5.3正弦函数的性质VIP免费

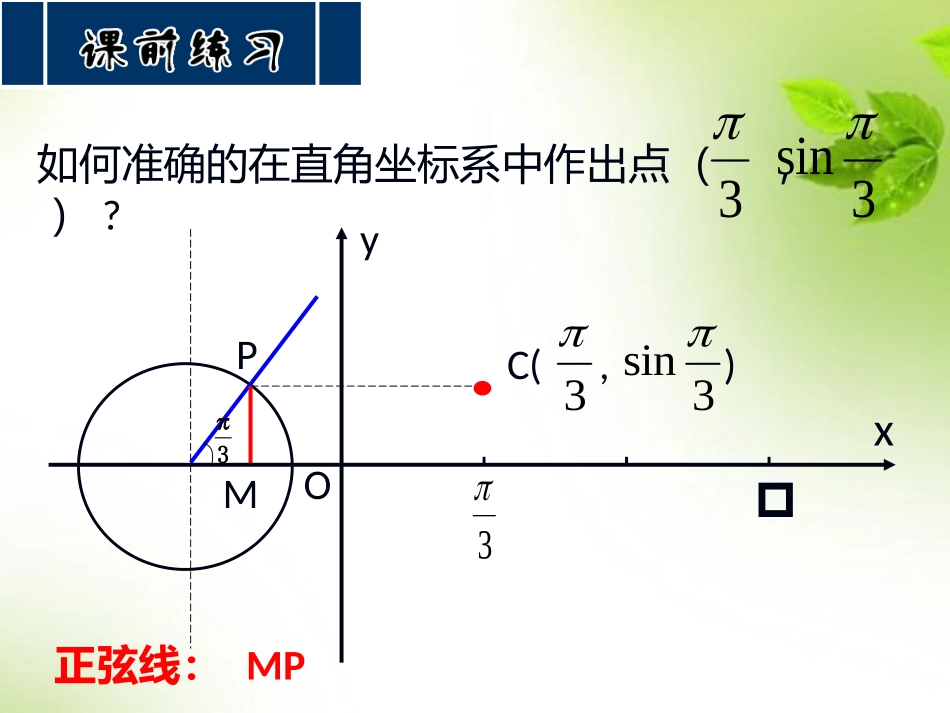
正弦函数y=sinx的图象与性质回顾：(1)正弦函数的定义；(2)画函数图像的一般步骤？如何准确的在直角坐标系中作出点（，）?3sin3PMC(,)33sinyxO3正弦线：MP3π新课探究新课探究2、用几何方法作正弦函数y=sinxx[0，]的图象：21-1022322656723352yx●●●332346116633265●●●●●●●673435611●●●这就是正弦函数y=sinx在x[0，]的图象。21-102322xy正弦函数的图象x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线yxo1-122322小飞守角制作2oxy---11--13232656734233561126sin[0,2]yxx在函数的图象上，起关键作用的点有：sin,[0,2]yxx最高点：最低点：与x轴的交点：(0,0)(,0)(2,0))1,(23)1,2(在精度要求不高的情况下，我们可以利用这5个点画出函数的简图，一般把这种画图方法叫“五点法画图”。x22322523yO23225311正弦函数sinyx定义域：值域：奇偶性：奇函数R[-1，1]周期：2ᴫ最大值：2x当时，有最大值1yk2最小值：2x当时，有最小值1yk2探究：正弦函数的单调性]2523[]22[]23,25[，、，、当在区间……上时，x曲线逐渐上升，sinα的值由增大到。11753357[,][][][,]22222222…、，、，、…当在区间x上时，曲线逐渐下降，sinα的值由减小到。11x22322523yO23225311递增区间)](22,22[Zkkk递减区间)](223,22[Zkkkx22322523yO23225311P'P正弦函数的图象53113,,,,22222x对称轴：,2xkkZ(,0),(0,0),(,0),(2,0)对称中心：(,0)kkZ例1：用“五点法”画出下列函数在区间[0，2π]的简图并讨论函数性质。xysin1)1(xysin3)3(xysin)2(．．．2．32xy0π．2π1-1xy=sinxx[0,2∈π]y=1+sinxx[0,2∈π]．．．2．32xy0π．2π1-1xy=sinxx[0,2∈π]y=—sinxx[0,2∈π]y=sin3xx[0,2∈π]．．．2．32xy0π．2π1-1x23练习：用“五点法”画出下列函数在一个周期内的的简图并研究函数的性质。xyxysin)2()4sin()1(作业：用“五点法”画出下面函数在区间[0，2π]的简图并讨论函数的性质。xxysinsin1：“五点法”作正弦函数图象；2：利用正弦函数图象研究函数性质3：函数的图形变换；寄语：用已有的知识方法去研究新的问题