正弦函数、余弦函数的图象VIP免费

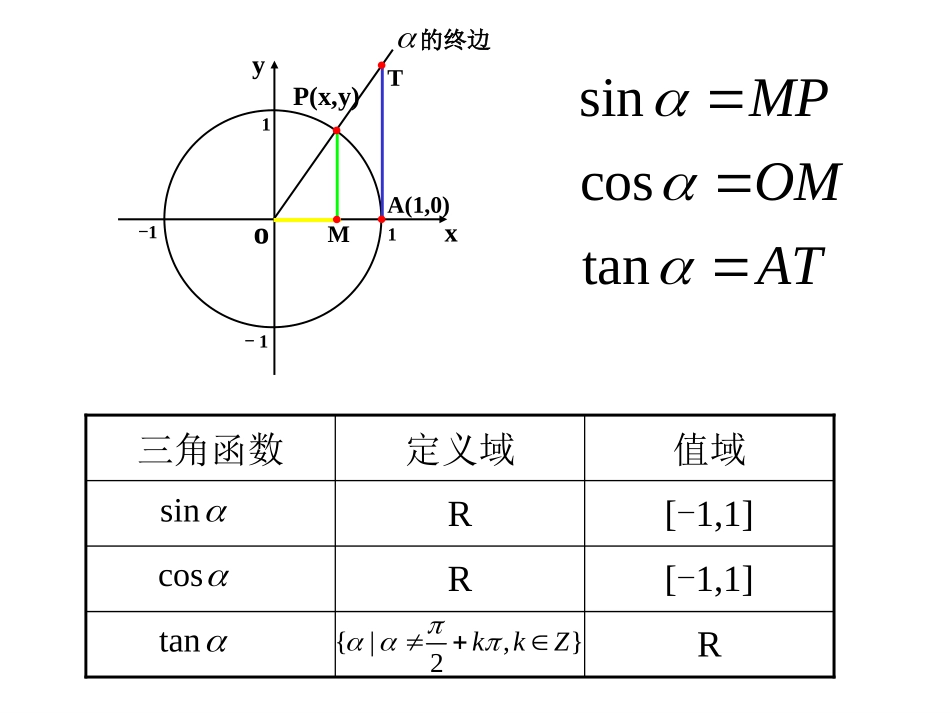
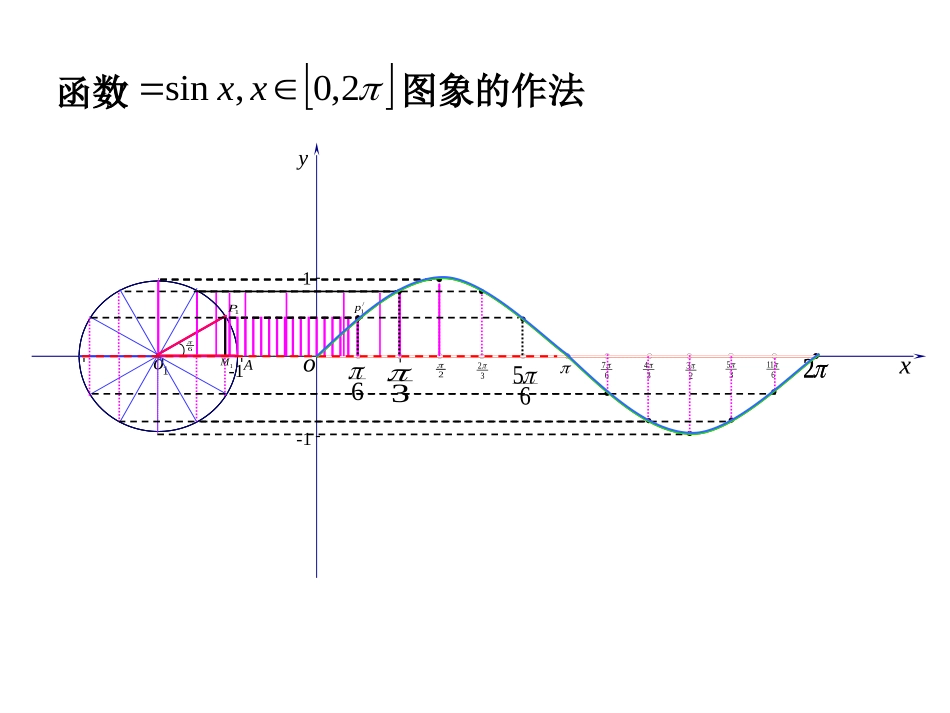
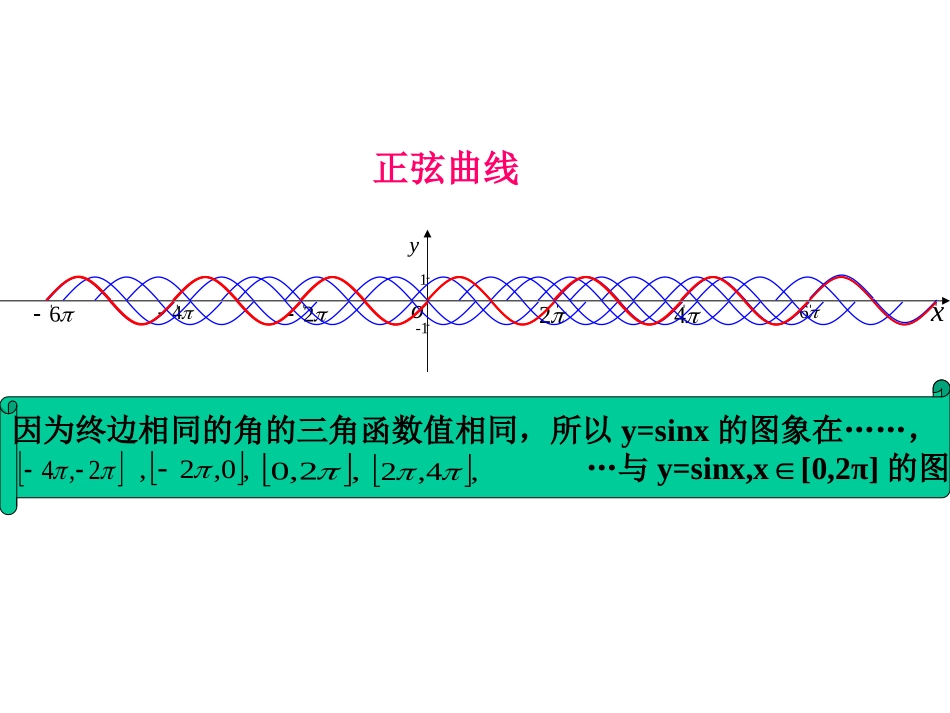
xyoP(x,y)1-11-1M的终边A(1,0)TsincostanMPOMATR[-1,1]R[-1,1]R值域定义域三角函数sincostan{|,}2kkZ232325667342335611262,0,sinxxy函数图象的作法oxy---11---1--1oA61P1M/1p因为终边相同的角的三角函数值相同，所以y=sinx的图象在……，…与y=sinx,x[0,2π]∈的图象相同2,4,0,2,,2,0,4,2正弦曲线xy---------1-12o46246xy1-1cossin()2yxx余弦曲线2余弦函数的图像可以通过正弦曲线向左平移各单位长度而得到．二、余弦函数y=cosx的图象正弦曲线：余弦曲线：sinyxxRcosyxxRxy1-1xy1-12oxy---11--13232656734233561126sin[0,2]yxx在函数的图象上，起关键作用的点有：sin,[0,2]yxx最高点：最低点：与x轴的交点：(0,0)(,0)(2,0))1,(23)1,2(在精度要求不高的情况下，我们可以利用这5个点画出函数的简图，一般把这种画图方法叫“五点法”。-oxy---11--13232656734233561126cos[0,2]yxx在函数的图象上，起关键作用的点有：cos,[0,2]yxx最高点：最低点：与x轴的交点：(0,1)3(,0)2(2,1)(,1)(,0)2正弦、余弦函数的图象例1画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-1012101o1yx22322-12y=sinx，x[0,2]y=1+sinx，x[0,2]步骤：1.列表2.描点3.连线正弦、余弦函数的图象例2画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]正弦、余弦函数的图象xsinx2230210-101例3在同一坐标系内，用五点法分别画出函数y=sinx，x[0,2]和y=cosx，x[,]的简图：223o1yx22322-12y=sinx，x[0,2]y=cosx，x[,]223向左平移个单位长度2xcosx100-1022302练习(1)作函数y=1+3cosx，x[0,2π]∈的简图(2)作函数y=2sinx-1，x[0,2π]∈的简图解：(1)解：(2)y0xΠΠ/23Π/22Π-3213-1-2y0xΠ/2Π3Π/22Π-23-1241正弦、余弦函数的性质x6yo--12345-2-3-41y=sinx(xR)x6o--12345-2-3-41yy=cosx(xR)定义域值域周期性R[-1,1]T=2正弦、余弦函数的奇偶性、对称性sin(-x)=-sinx(xR)y=sinx(xR)x6yo--12345-2-3-41是奇函数x6o--12345-2-3-41ycos(-x)=cosx(xR)y=cosx(xR)是偶函数定义域关于原点对称正弦、余弦函数的奇偶性正弦、余弦函数的单调性正弦函数的单调性y=sinx(xR)增区间为[，]其值从-1增至122xyo--1234-2-31223252722325xsinx2223…0………-1010-1减区间为[，]其值从1减至-1223[+2k,+2k],kZ22[+2k,+2k],kZ223正弦、余弦函数的单调性余弦函数的单调性y=cosx(xR)xcosx22-……0……-1010-1增区间为其值从-1增至1[+2k,2k],kZ减区间为，其值从1减至-1[2k,2k+],kZyxo--1234-2-31223252722325正弦、余弦函数的奇偶性、单调性例1不通过求值，指出下列各式大于0还是小于0：(1)sin()–sin()1810(2)cos()-cos()523417解：218102又y=sinx在上是增函数]2,2[sin()01810解：5340cos