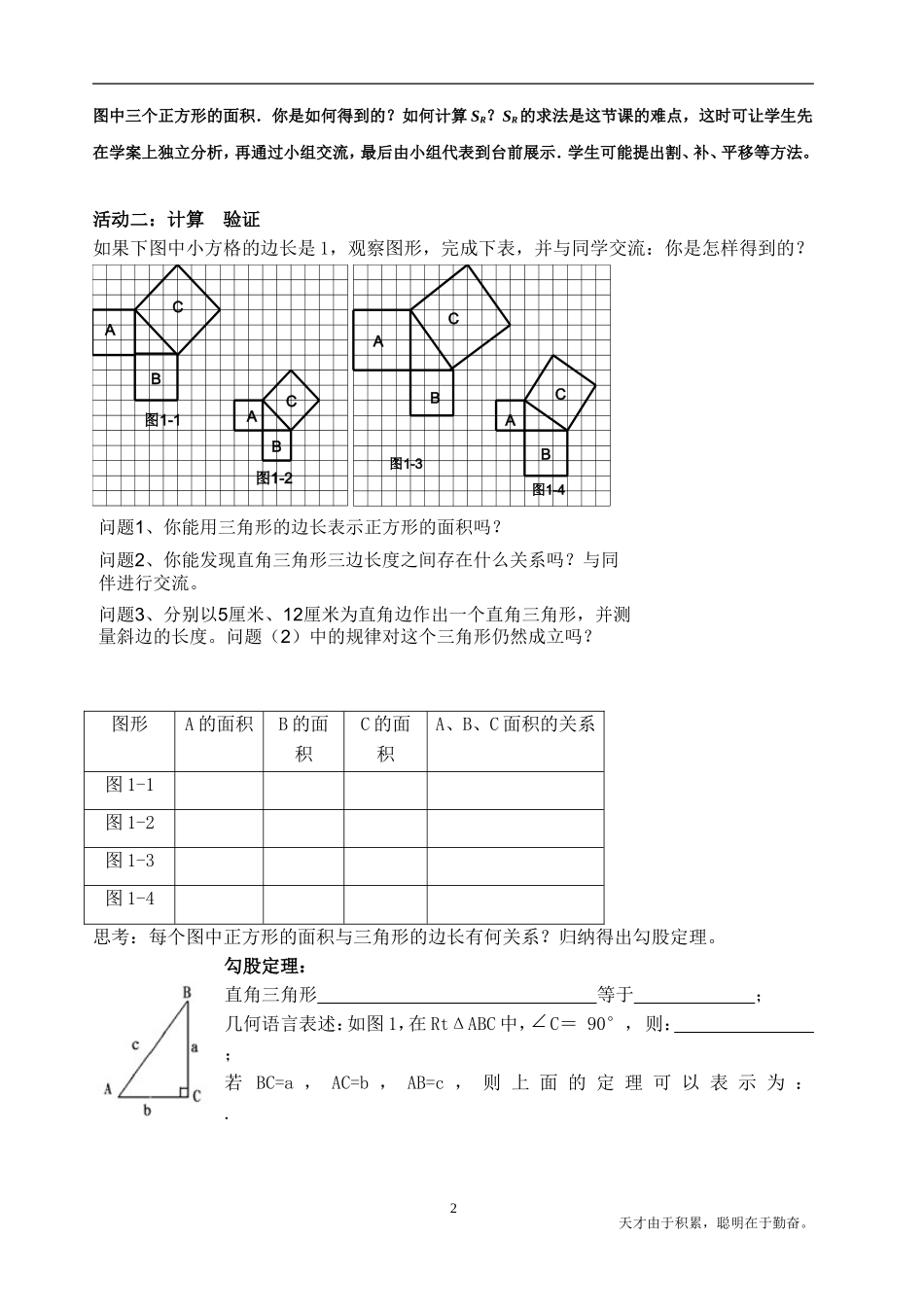
1(每一个小正方形的边长记作“1”)RQPBCA镇江市第十中学生本课堂八年级数学教案使用时间:月日3.1勾股定理(1)主备:蒋苏青审核:班级姓名教学目标:1.经历探索勾股定理的过程,发展学生的合情推理意识,体会数形结合的思想.2.会初步利用勾股定理解决实际问题.教学过程:一、课前准备:(梳理学生已有的对于直角三角形的相关知识,引入课题)1.三角形按角的大小可分为:、、.2.在RtΔABC中,两条直角边长分别为a、b,则这个直角三角形的面积可以表示为:.3.直角三角形的两个锐角.4.三角形的三边关系:三角形的任意两边之和;任意两边之差.(学生回顾知识后,教师启发引导:1.如果一个三角形的两条边分别长6和8,你知道第三边的长吗?你知道第三边长的范围吗?2.如果又已知这两边的夹角是90度,那么第三边的长确定吗?3.已知直角三角形的两边的长,如何求第三边的长呢?这节课就让我们一起来探讨这个问题.板书:直角三角形三边数量关系.)二、探索活动活动一、观察猜想:观察这枚邮票上的图案和图案中各正方形内小方格的个数,猜想:这三个三角形的面积有何关系?W1.用什么方法来探求?我们曾经利用图形面积探索过数学公式,大家还记得在哪用过吗?例如平方差公式、完全平方公式、单项式乘多项式、多项式乘多项式.2.为了计算面积方便,我们可将这幅图形放在方格纸中.如果每一个小方格的边长记作“1”,请你求出(图1)2图中三个正方形的面积.你是如何得到的?如何计算SR?SR的求法是这节课的难点,这时可让学生先在学案上独立分析,再通过小组交流,最后由小组代表到台前展示.学生可能提出割、补、平移等方法。活动二:计算验证如果下图中小方格的边长是1,观察图形,完成下表,并与同学交流:你是怎样得到的?ABCACB图1-1图1-2ABCACB图1-3图1-4问题1、你能用三角形的边长表示正方形的面积吗?问题2、你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。问题3、分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。问题(2)中的规律对这个三角形仍然成立吗?图形A的面积B的面积C的面积A、B、C面积的关系图1-1图1-2图1-3图1-4思考:每个图中正方形的面积与三角形的边长有何关系?归纳得出勾股定理。勾股定理:直角三角形等于;几何语言表述:如图1,在RtΔABC中,C=90°,则:;若BC=a,AC=b,AB=c,则上面的定理可以表示为:.天才由于积累,聪明在于勤奋。3ABCD7cm镇江市第十中学生本课堂八年级数学教案使用时间:月日三、知识应用:1.课本79-80练习1、2、32.在△ABC中,∠C=90°,www.12999.com(1)若BC=6,AC=8,则AB=;(2)若BC=4,AB=5,则AC=;(3)若BC∶AC=3∶4,AB=20,则BC=,AC=;(评讲时可追问,你会求此三角形斜边上的高吗?)3.如图所示,强大的台风使得一根旗杆在离地面9米处折断倒下,旗杆顶部落在离旗杆底部12米处。旗杆折断之前有多高?四、课后巩固:1.在△ABC中,∠C=90°,www.12999.com(1)若BC=5,AC=12,则AB=;(2)若BC=3,AB=5,则AC=;(3)若BC∶AC=3∶4,AB=10,则BC=,AC=;(4)若AB=8.5,AC=7.5,则BC=.2.某农舍的大门是一个木制的矩形栅栏,它的高为2m,宽为1.5m,现需要在相对的顶点间用一块木棒加固,木棒的长为.3.在Rt△ABC中,∠C=90°,AC=5,AB=13,则BC=,该直角三角形的面积为.4.直角三角形两直角边长分别为5cm,12cm,则斜边上的高为..5.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_______cm2.教学反思: