高中二年级数学选修2课件VIP免费

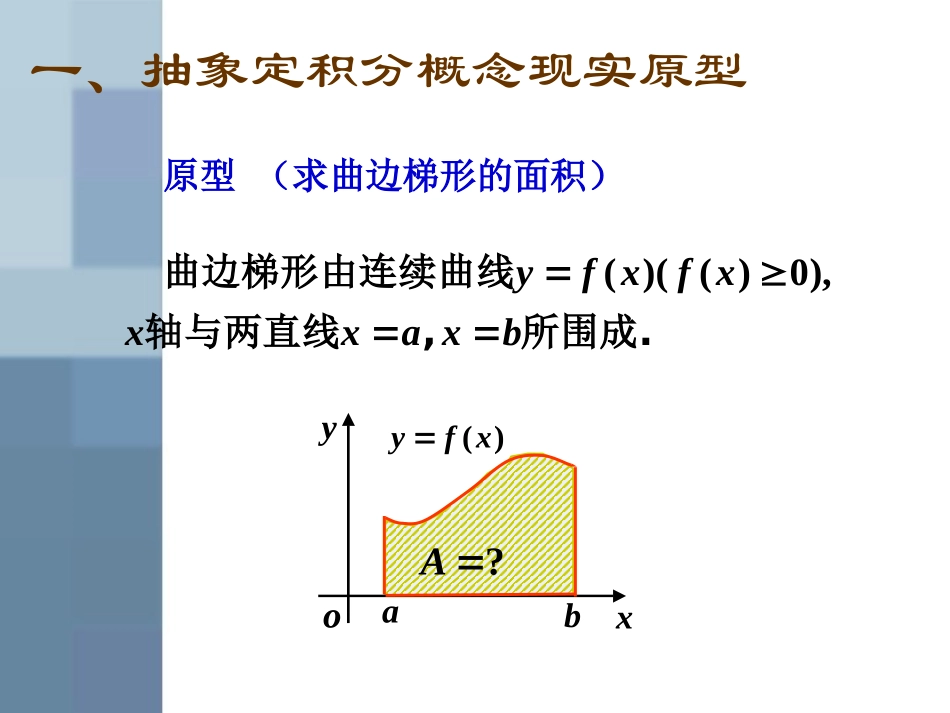
定积分的概念abxyo?A原型（求曲边梯形的面积）一、抽象定积分概念现实原型)(xfy曲边梯形由连续曲线轴与两直线,所围成.()(()0),yfxfxxxaxb考察下列图形由哪些曲边围成.A2022xy00yAsinyx0x面积怎么求？面积怎么求？元素法元素法2xππxπ2y0x利用元素法的思想求解曲边梯形的面积时，可概括“分割-取近似-求和-取极限”的步骤.将曲边梯形的底，即[a,b]进行分割(用垂直于x轴的直线).第一步分割；第一步分割；曲边梯形的面积的解决思路：abxyo)(xfyix1x1ix1nx2x记1.iiixxx取出典型小区域，用矩形面积近似曲边梯形面积.第二步取近似；第二步取近似；abxyo)(xfy用矩形面积近似用矩形面积近似小曲边梯形面积小曲边梯形面积()if高底ix1x1ix1nx2xix典型小区域面积iSi().iiiSfxabxyo)(xfyix1x1ix1nx2x第三步求和；第三步求和；i矩形面积和与曲边梯形面积不相等有误差有误差121nn11().nniiiiiSfx将每个小曲边梯形的面积都用矩形近似，并将所有的小矩形面积加起来.第四步取极限.第四步取极限.当对曲边梯形底的分割越来越细时，矩形面积之和越近似于曲边梯形面积.abxyo)(xfy0,1,2,,ixinmax{}0ix11()nniiiiiASfx112233()()()(),nnfxfxfxfxiniixfA)(lim101122330lim[()()()()].nnfxfxfxfx曲边梯形面积的近似值为:曲边梯形面积为当即小区间的最大长度趋近于零时分割无限加细12,max{,,,}(0),nxxx设是定义在区间上的有界函数用点将区间任意分割成个子区间这些子区间及其长度均记作在每一子区间上任取一点作个乘积的和式012111()[,],...[,][,](1,2,...),(1,2,...,).,()nniiiiiiiiifxabaxxxxxbabnxxixxxinxnfx二、定积分的定义1().niiifx定义以直代曲求和被积函数被积表达式[,]ab为积分区间积分上限积分下限如果当同时最大子区间的长度时和式并且其极限值与的分割法以及的取法无关则该极限值称为函数区间在上的定积分记作的极限存在1,max{}0,,[,],[,]()(,:)niiiiifxfxnxabab1(0)()lim()nbiianifxxfxd积分变量积分和()fxx取极限即注意：()baxfxd()bafttd()bafuud(2).i在定义中区间的分法和的取法是任意的(1),.积分值仅与被积函数及积分区间有关而与积分变量的字母无关(3)()[,],()[,]fxabfxab当函数在区间上的定积分存在时称在区间上可积.xtuxtu,0)(xf()bafxxAd曲边梯形的面积,0)(xfd()bafxxA曲边梯形的面积的负值1234()bafxxAAAAd定积分的几何意义3A4A2A1AabyxO几何意义(),;xfxxaxbxx它是介于轴、函数的图形及两条直线之间的各部分面积的代数和．在轴上方的面积取正号在轴下方的面积取负号．__abyxO例1利用定积分的几何意义计算下列积分dd11200.(1);(2)1.xxxx解d，10(1)xx表示由及轴围成的三角形面积.0,1,xxyxx100x1x0yAyxd10xx11121.2d120(2)1,xx表示由及轴围成的圆面积.20,1,114xxyxx100x1x0yd1201xx1.4yxA2114π定理()[,],,()[,()()].,bbaafxabkkfxkffaxbxxkx若在上可积为常数则在上dd也可积且三、定积分的性质定理()[,],()()[,],(()())()().bbbaaafxgxxfxabfxgfbxxgxxxa若在上可积则在上也可积且ddd补充：不论的相对位置如何,上式总成立.cba,,定理（积分区间的可加性）ddd323002()()(),fxxfxxfxxddd363006()()(),fxxfxxfxx有界函数在上都可积的充要条件是在上也可积且ddd()[,],[,]()[,]()()(),.bcbaacfxxfxxffxaccbfxaxxb2660320632abcSacScbSabdd1.bbaaxxba定理d203xπd2033.2xππ对定积分的补充规定:(1),()0.baabfxx当时令d(2)(),()().abbaababfxxfxxfxx当且d存在时则dd定理（保序性）推论（保号性）()()()()[,],(),[,],().bbaafxgxabgxfxgxxf...