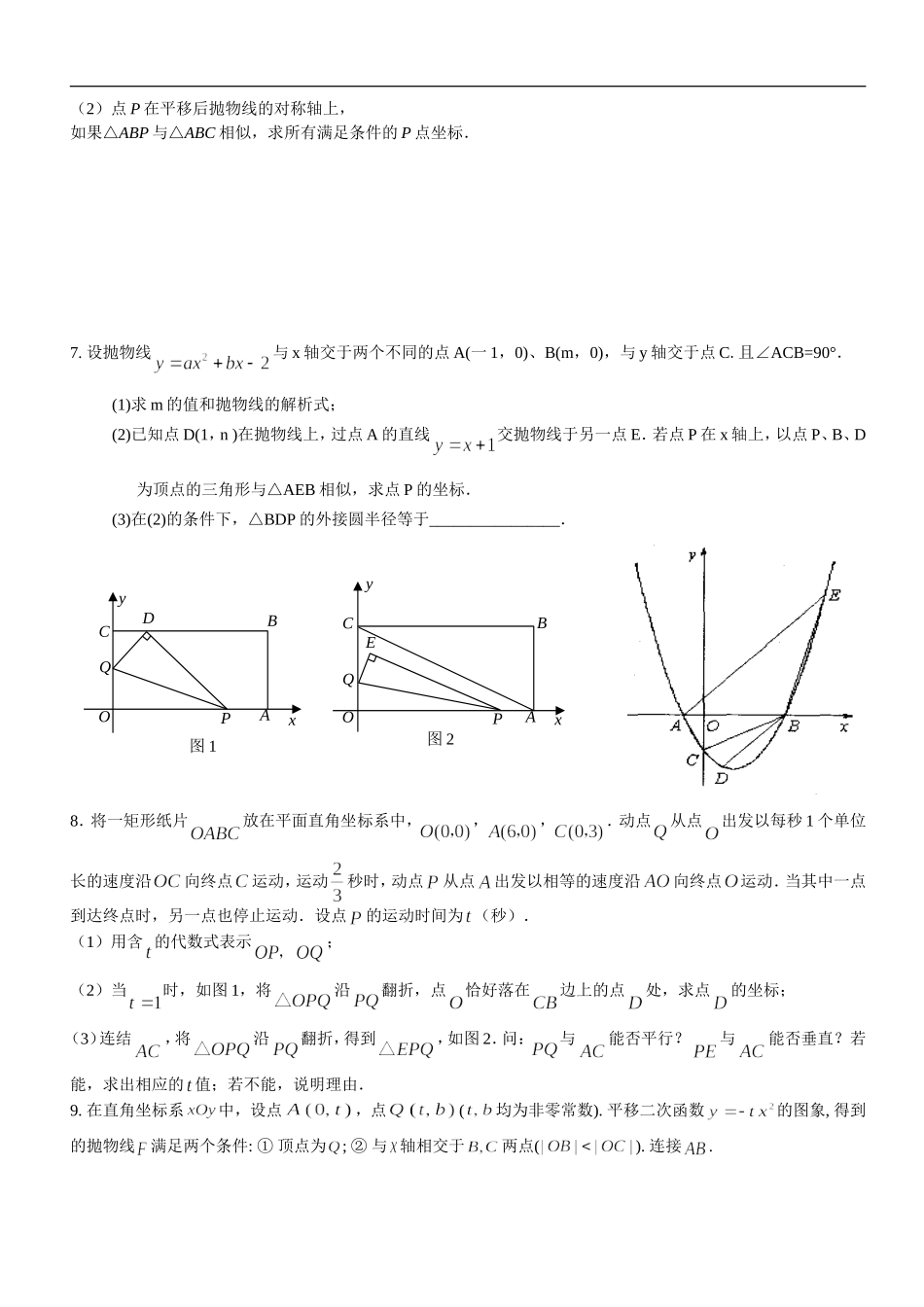
OyxDCBA教师:学生:时间:年月日段动点产生相似问题1.已知∠AOB=45°,P是边OA上一点,OP=,以点P为圆心画圆,圆P交OA于点C(点P在O、C之间,如图)点Q是直线OB上的一个动点,连PQ,交圆P于点D,已知,当OQ=7时,,(1)求圆P半径的长;(2)当点Q在射线OB上运动时,以点Q为圆心,OQ为半径作圆Q,若圆Q与圆P相切,试求OQ的长度;(3)连CD并延长交直线OB于点E,是否存在这样的点Q,使得以O、C、E为顶点的三角形与△OPQ相似,若存在,试确定Q点的位置;若不存在,试说明理由。2.已知:如图,在平面直角坐标系中,是直角三角形,,点的坐标分别为,,∠BAC的正切值是3/4(1)求过点的直线的函数解析式;(2)在轴上找一点,连接,使得与相似(不包括全等),并求点的坐标;(3)在(2)的条件下,如果分别是和上的动点,连接,设,问是否存在这样的,使得与相似,如存在,请求出的值;如不存在,请说明理由.3.如图,双曲线和在第二象限中的图像,A点在的图像上,点A的横坐标为m(m<0),AC∥y轴交图像于点C,AB、DC均平行x轴,分别交、的图像于点B、D.ACOBxyOCQBAPDECQBAOPD(1)用m表示A、B、C、D的坐标;(2)求证:梯形ABCD的面积是定值;(3)若△ABC与△ACD相似,求m的值.4.如图,直线(>)与分别交于点,,抛物线经过点,顶点在直线上.(1)求的值;(2)求抛物线的解析式;(3)如果抛物线的对称轴与轴交于点,那么在对称轴上找一点,使得和相似,求点的坐标.5.如图所示,抛物线(m>0)的顶点为A,直线l:与y轴交点为B.(1)写出抛物线的对称轴及顶点A的坐标(用含m的代数式表示);(2)证明点A在直线l上,并求∠OAB的度数;(3)动点Q在抛物线对称轴上,问抛物线上是否存在点P,使以点P、Q、A为顶点的三角形与⊿OAB全等?若存在,求出m的值,并写出所有符合上述条件的P点坐标;若不存在,请说明理由.6.在平面直角坐标系中,将抛物线沿轴向上平移1个单位,再沿轴向右平移两个单位,平移后抛物线的顶点坐标记作A,直线与平移后的抛物线相交于B,与直线OA相交于C.(1)求△ABC面积;ABOxyBAyx第25题图y=-x-3m2l:y=33x-mO12345-1-2-3-4-5-1-2-3-4-512345xy0(2)点P在平移后抛物线的对称轴上,如果△ABP与△ABC相似,求所有满足条件的P点坐标.7.设抛物线与x轴交于两个不同的点A(一1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.(1)求m的值和抛物线的解析式;(2)已知点D(1,n)在抛物线上,过点A的直线交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.(3)在(2)的条件下,△BDP的外接圆半径等于________________.8.将一矩形纸片放在平面直角坐标系中,,,.动点从点出发以每秒1个单位长的速度沿向终点运动,运动秒时,动点从点出发以相等的速度沿向终点运动.当其中一点到达终点时,另一点也停止运动.设点的运动时间为(秒).(1)用含的代数式表示;(2)当时,如图1,将沿翻折,点恰好落在边上的点处,求点的坐标;(3)连结,将沿翻折,得到,如图2.问:与能否平行?与能否垂直?若能,求出相应的值;若不能,说明理由.9.在直角坐标系中,设点,点(均为非零常数).平移二次函数的图象,得到的抛物线满足两个条件:①顶点为;②与轴相交于两点().连接.图1OPAxBDCQy图2OPAxBCQyE(1)是否存在这样的抛物线,使得请你作出判断,并说明理由;(2)如果,且,求抛物线对应的二次函数的解析式.10.已知:抛物线(a≠0),顶点C(1,),与x轴交于A、B两点,.(1)求这条抛物线的解析式.(2)如图,以AB为直径作圆,与抛物线交于点D,与抛物线对称轴交于点E,依次连接A、D、B、E,点P为线段AB上一个动点(P与A、B两点不重合),过点P作PM⊥AE于M,PN⊥DB于N,请判断是否为定值?若是,请求出此定值;若不是,请说明理由.(3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP,FG分别与边AE、BE相交于点F、G(F与A、E不重合,G与E、B不重合),请判断是否成立.若成立,请给出证明;若不成立,请说明理由.11.抛物线(1)(5)yaxx与x轴的交点为M、N.直线ykxb与x轴交于P(-2,0).与y轴交于C,若A、B两点在直线ykxb上.且AO=BO=2,...