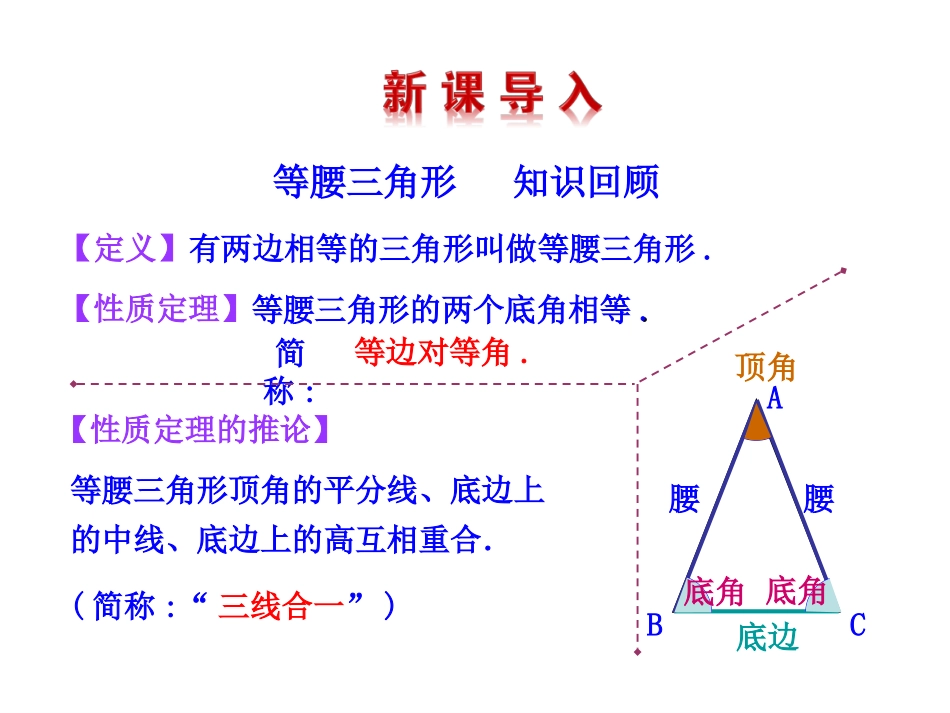
第2课时1.你能证明它们吗1.掌握证明的基本步骤和书写格式;2.经历“探索、猜想、证明”的过程,能够用综合法证明等腰三角形的有关性质定理和判定定理;3.结合实例体会反证法的含义.等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合.等腰三角形的两个底角相等..简称:等边对等角.顶角ABC底边腰腰底角底角【定义】【性质定理】【性质定理的推论】有两边相等的三角形叫做等腰三角形.(简称:“三线合一”)等腰三角形知识回顾ACB你能证明你的结论吗?画一画:先画一个等腰三角形,然后在等腰三角形中作出一些线段(如角平分线、中线、高线),你能发现其中一些相等的线段吗?等腰三角形还具有哪些重要的性质?除了用定义来判定三角形是等腰三角形外,还有哪些简单的方法来判定三角形是等腰三角形?结论1.三线合一2.底角的两条平分线相等3.两条腰上的中线相等4.两条腰上的高线相等图例ADCBACBDEACBMNACBQP【结论】【例1】证明:等腰三角形两底角的平分线相等.ACBDE已知:求证:BD=CE.如图,在△ABC中,AB=AC,BD,CE是△ABC角平分线.12【例题】 AB=AC(已知),∴∠ABC=∠ACB(等边对等角).【证明】21∠2=∠ACB(已知),又 ∠1=∠ABC,21∴∠1=∠2(等式性质).在△BDC与△CEB中 ∠DCB=∠EBC(已知),BC=CB(公共边),∠1=∠2(已证),∴△BDC≌△CEB(ASA).∴BD=CE(全等三角形的对应边相等).ACBDE121.证明:等腰三角形两腰上的高相等.【证明】 AB=AC(已知),∴∠ABC=∠ACB(等边对等角).又 BP,CQ是△ABC两腰上的高(已知),∴∠BPC=∠CQB=90°(高的意义).在△BPC与△CQB中 ∠BPC=∠CQB(已证),∠PCB=∠QBC(已证),BC=CB(公共边),∴△BPC≌△CQB(AAS).∴BP=CQ(全等三角形的对应边相等).已知:如图,在△ABC中,AB=AC,BP,CQ是△ABC两腰上的高.求证:BP=CQ.ACBPQ【跟踪训练】又 CM=,BN=(已知),1AB22.证明:等腰三角形两腰上的中线相等.BM=CN.求证:已知:如图,在△ABC中,AB=AC,BM,CN是△ABC两腰上的中线.AC21【证明】 AB=AC(已知),∴∠ABC=∠ACB(等边对等角).(全等三角形的对应边相等).∴CM=BN(等式的基本性质).在△BMC与△CNB中 BC=CB(公共边),∠MCB=∠NBC(已知),CM=BN(已证),∴△BMC≌△CNB(SAS).∴BM=CN.ACBMNACBDE1.已知:如图,在△ABC中,AB=AC(1)如果∠ABD=∠ABC,∠ACE=∠ACB,那么BD=CE吗?为什么?(2)如果∠ABD=∠ABC,∠ACE=∠ACB呢?由此你能得到一个什么结论?如果∠ABD=∠ABC,∠ACE=∠ACB,那么BD=CE吗?【议一议】121213131n1n2.已知:如图,在△ABC中,AB=AC如果AD=AC,AE=AB,那么BD=CE吗?为什么?ACBDE由此你能得到一个什么结论?如果AD=AC,AE=AB,那么BD=CE吗?数学方法:特殊到一般的思想方法12121n1n3.“”“前面已经证明了等边对等角,反过来,等角对”等边吗?即有两个角相等的三角形是等腰三角形吗?ACB已知:如图,在△ABC中,∠B=∠C.求证:AB=AC.要证明AB=AC,只要能构造出AB,AC所在的两个三角形全等就可以了.请与小组内同学交流.分析:作∠A的平分线或作BC边上的高.作BC边上的中线可以吗?有两个角相等的三角形是等腰三角形(等角对等边).这又是判定两条线段相等的依据之一.请同学们注意运用哦!等腰三角形的判定定理在△ABC中 ∠B=∠C(已知),∴AB=AC(等角对等边).AACCBB【结论】两个角相等的三角形是等腰三角形,那么在一个三角形中,如果两个角不相等,那么这两个角所对的边有什么关系呢?CCAABB你认为这个结论成立吗?如果成立,你能证明它吗?请与小组内同学交流.在△ABC中,如果∠B≠∠C,那么AC≠AB.也不相等?【猜想】CAB分析:如图,在△ABC中,已知∠B≠∠C,此时,AC与AB要么相等,要么不相等.证明:假设AB=AC,那么根据“等边对等角”定理可得∠B=∠C,但已知条件是∠B≠∠C.“∠B=∠C”与“∠B≠∠C”相矛盾,因此,AB≠AC.论证命题的新思维与新方法先假设命题的结论不成立,然后推导出与定义、公理、已证定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.这种证明方法称为反证法.(reductiontoabsurdity)反证法是一种重要的数学证明方法,在解决某些问题时常常会有出人意料的作用.论证的新方法----反证法...