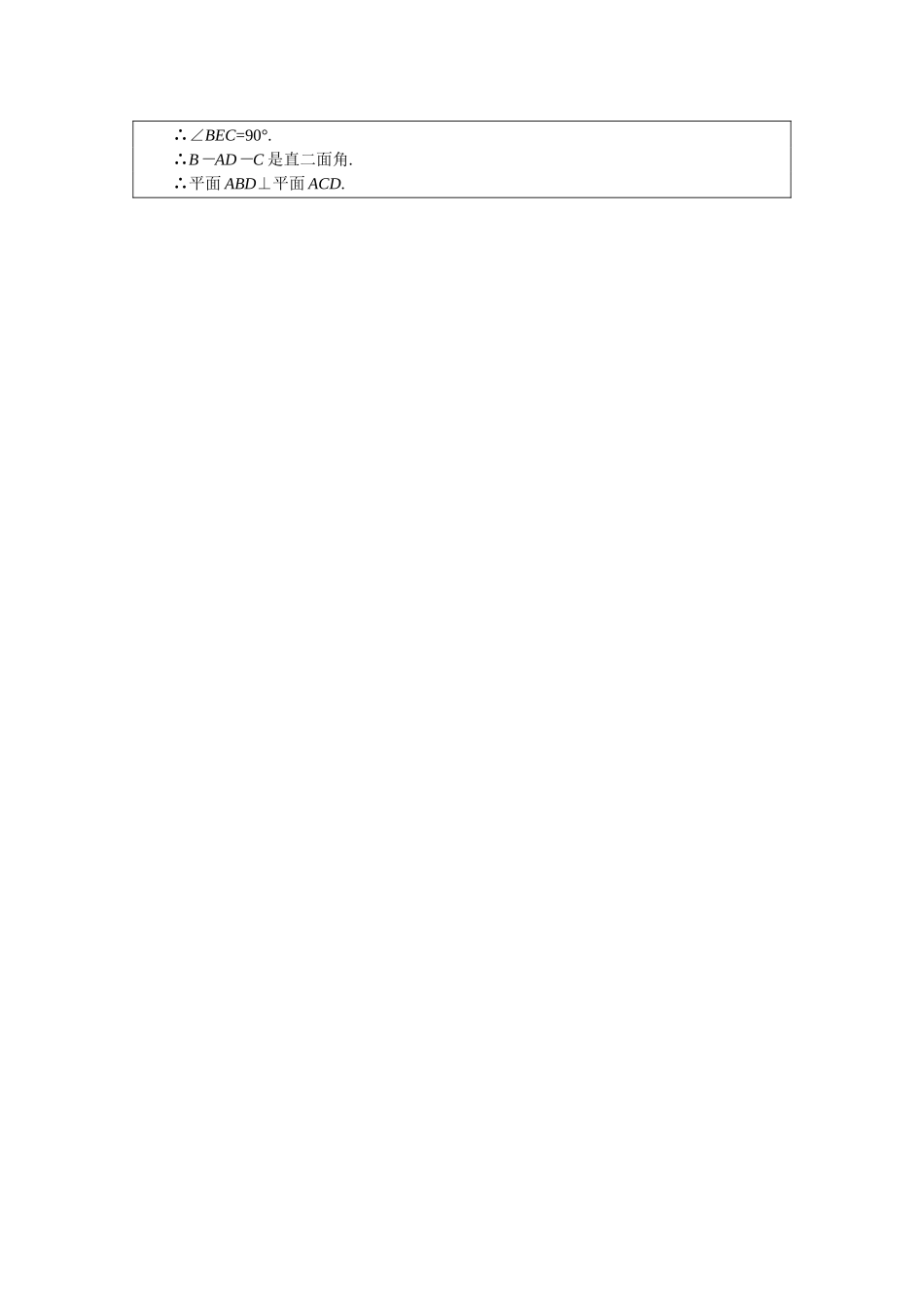
一课一测一、选择题1.关于正多面体的概念,下面叙述中正确的是()A.每个面都是正多边形的多面体B.每个面都是有相同边数的正多边形的多面体C.每个面都是有相同边数的正多边形,且以每个顶点为其一端都有相同数目的棱的多面体D.每个面都是有相同边数的正多边形,且以每个顶点为其一端都有相同数目的棱的凸多面体2.下列命题中,假命题是()①多面体的面数最少是4②正多面体只有5种③凡凸多面体都是简单多面体④一个几何体的表面经过连续变形能变为球面的就叫简单多面体A.③B.②③C.④D.③④3.设正多面体的每个面都是正n边形,以每个顶点为端点的棱有m条,顶点数是V,棱数是E,面数是F,则它们之间的关系不正确的是()A.mF=2EB.nF=2EC.mV=2ED.V+F=E+24.正十二面体的顶点V和棱数E分别是()A.V=30E=20B.V=12E=30C.V=30E=12D.V=20E=305.如图9-研-6,正方体的棱长为3cm,在每一个面的正中间有一个正方形孔通到对面,孔的边长为1cm,孔的各棱平行于正方体的各棱,则此时该几何体的总表面积为()图9-研-6A.54cm2B.72cm2C.76cm2D.84cm26.图9-研-7中多面体是过正四棱柱的底面正方形ABCD的点A作截面AB1C1D1而截得的,且B1B=D1D.已知截面AB1C1D1与底面ABCD成30°的二面角,AB=1,则这个多面体的体积为()图9-研-7A.B.C.D.二、填空题7.一个简单多面体的各面都是三角形,它的顶点数为12,则它的面数为.8.每个面都是正三角形,每个顶点出发都有三条棱的多面体,其面数F=,顶点数V=,棱数E=.9.棱长为a的正八面体的对角线长为.10.已知一个正多面体的体积为V,它的一个侧面面积为S,则由正多面体内一点到各侧面的距离之和等于.三、解答题11.C70分子有类似于C60的球状多面体结构,它有70个顶点,每个顶点处有3条棱,各个面是五边形或六边形,试求C70分子结构中,有多少个五边形,有多少个六边形?12.一个正多面体,各个面的内角总和为3600°,求它的面数、顶点数和棱数.13.四面体ABCD的6条棱中除AD外,其他5条棱的长度均为1.(1)当AD长度变化时,求四面体全面积的最大值;(2)当此四面体全面积最大时,平面ABD与平面ACD的位置关系如何?参考答案一、1.D2.C3.A4.D5.B6.D二、7.208.4469.a10.11.解:设C70分子中形状为五边形和六边形的面各有x个和y个,则三、解得x=12,y=25.∴有12个五边形,25个六边形.12.解:设正多面体共有n个面,每边是m边形,则(m-2)·180°=,∴m-2=.∵m只能为3,4,5,n只能为4,6,8,12,20,∴n=20,m=3故该正多面体是正20面体.面数F=20,顶点数V=12,棱数E=30.13.解:(1)当∠ABD=∠ACD=90°时,四面体的全面积最大,为+1.(2)设AD的中点为E,则BE⊥AD,CE⊥AD,BE=CE=,BC=1.∴∠BEC=90°.∴B-AD-C是直二面角.∴平面ABD⊥平面ACD.