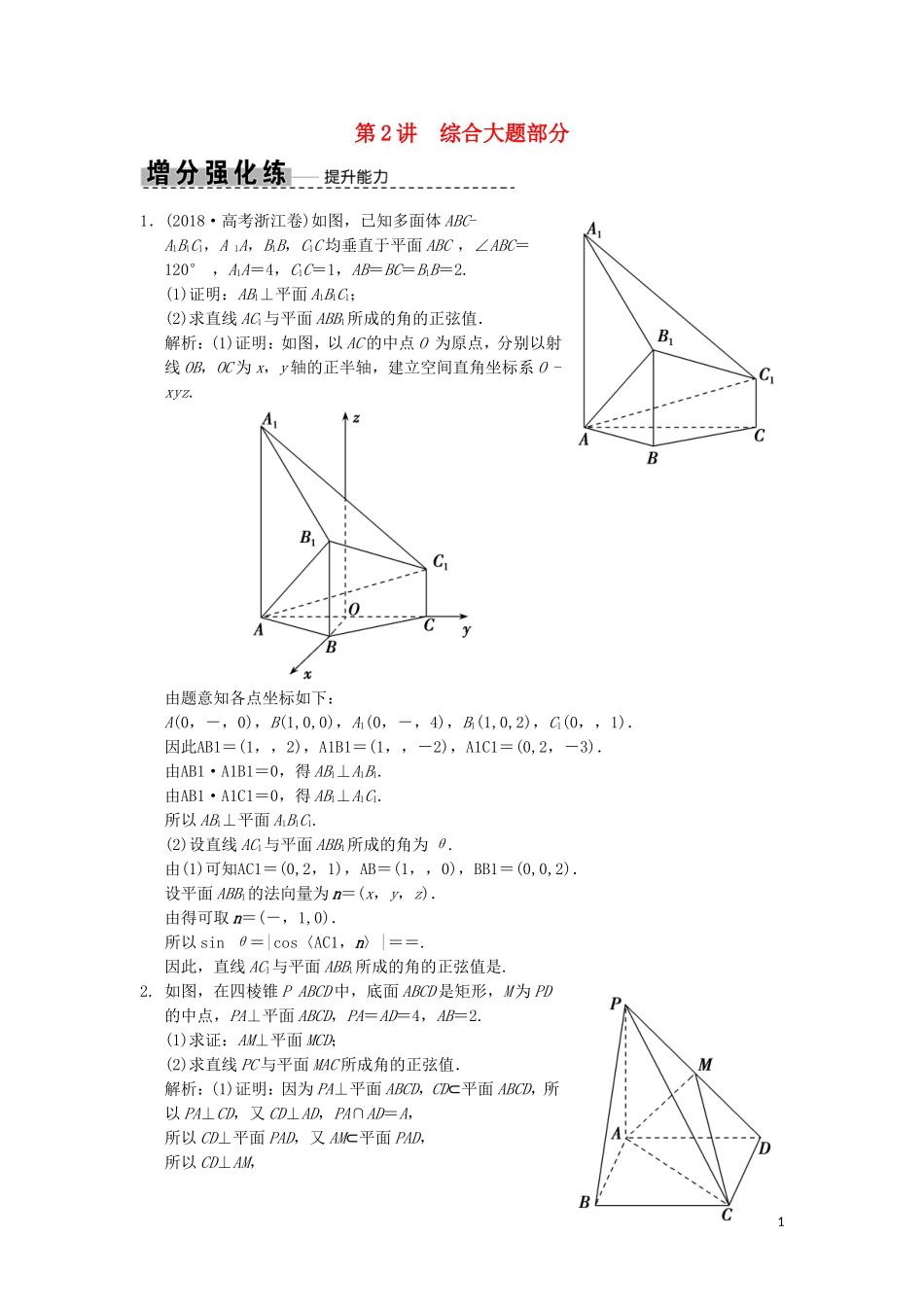
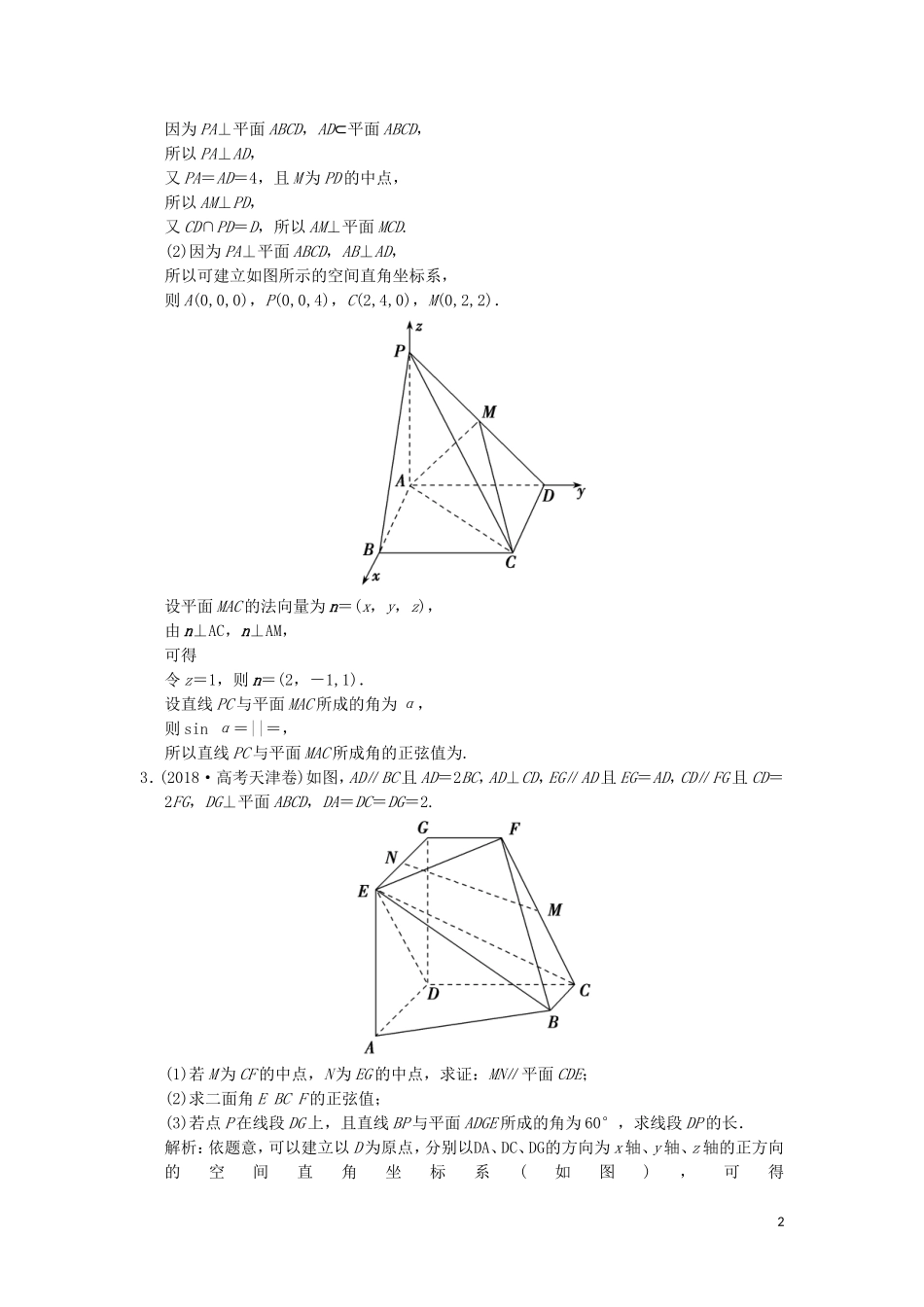
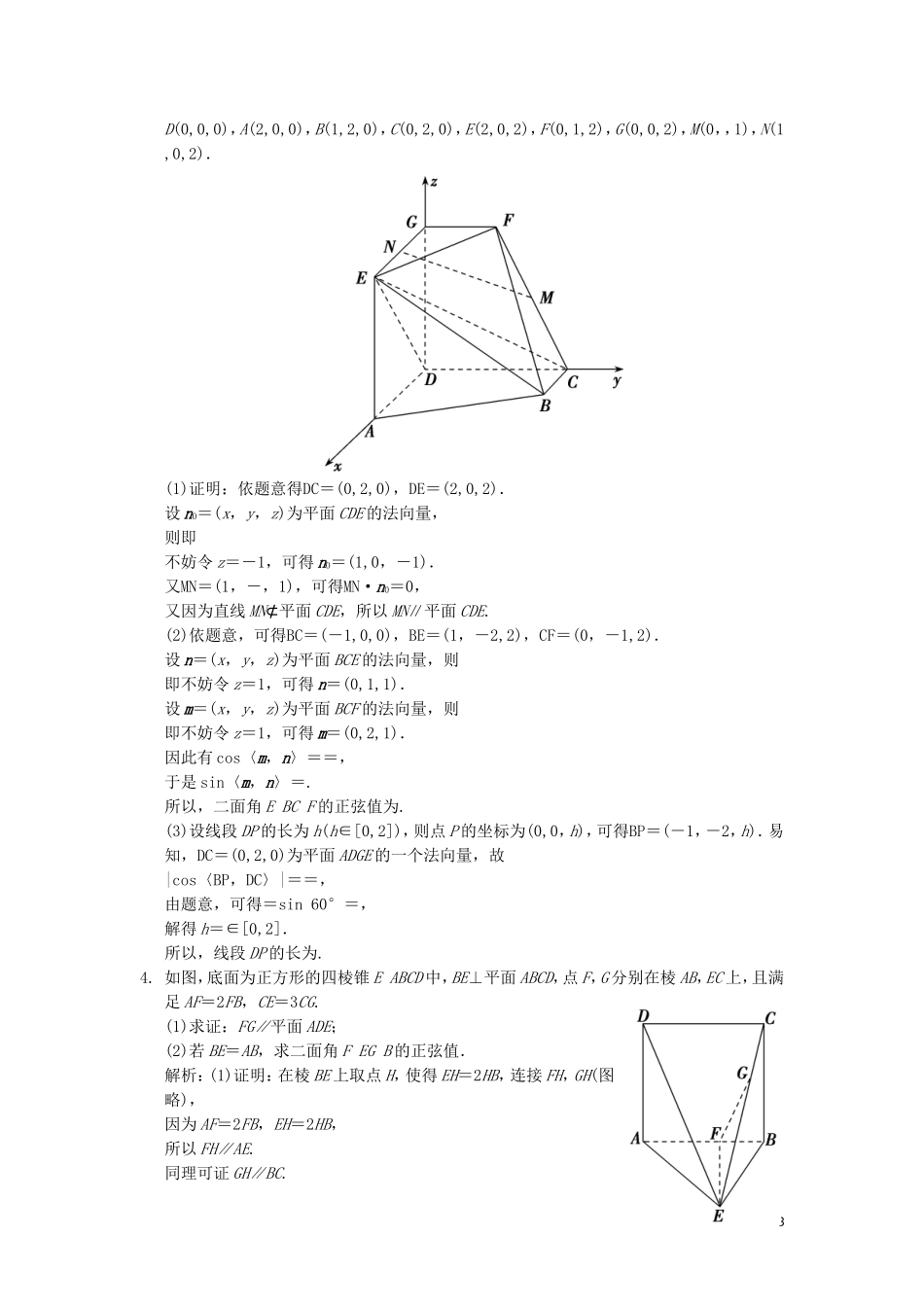
第2讲综合大题部分1.(2018·高考浙江卷)如图,已知多面体ABC-A1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.解析:(1)证明:如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的正半轴,建立空间直角坐标系O-xyz.由题意知各点坐标如下:A(0,-,0),B(1,0,0),A1(0,-,4),B1(1,0,2),C1(0,,1).因此AB1=(1,,2),A1B1=(1,,-2),A1C1=(0,2,-3).由AB1·A1B1=0,得AB1⊥A1B1.由AB1·A1C1=0,得AB1⊥A1C1.所以AB1⊥平面A1B1C1.(2)设直线AC1与平面ABB1所成的角为θ.由(1)可知AC1=(0,2,1),AB=(1,,0),BB1=(0,0,2).设平面ABB1的法向量为n=(x,y,z).由得可取n=(-,1,0).所以sinθ=|cos〈AC1,n〉|==.因此,直线AC1与平面ABB1所成的角的正弦值是.2.如图,在四棱锥PABCD中,底面ABCD是矩形,M为PD的中点,PA⊥平面ABCD,PA=AD=4,AB=2.(1)求证:AM⊥平面MCD;(2)求直线PC与平面MAC所成角的正弦值.解析:(1)证明:因为PA⊥平面ABCD,CD⊂平面ABCD,所以PA⊥CD,又CD⊥AD,PA∩AD=A,所以CD⊥平面PAD,又AM⊂平面PAD,所以CD⊥AM,1因为PA⊥平面ABCD,AD⊂平面ABCD,所以PA⊥AD,又PA=AD=4,且M为PD的中点,所以AM⊥PD,又CD∩PD=D,所以AM⊥平面MCD.(2)因为PA⊥平面ABCD,AB⊥AD,所以可建立如图所示的空间直角坐标系,则A(0,0,0),P(0,0,4),C(2,4,0),M(0,2,2).设平面MAC的法向量为n=(x,y,z),由n⊥AC,n⊥AM,可得令z=1,则n=(2,-1,1).设直线PC与平面MAC所成的角为α,则sinα=||=,所以直线PC与平面MAC所成角的正弦值为.3.(2018·高考天津卷)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;(2)求二面角EBCF的正弦值;(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.解析:依题意,可以建立以D为原点,分别以DA、DC、DG的方向为x轴、y轴、z轴的正方向的空间直角坐标系(如图),可得2D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),E(2,0,2),F(0,1,2),G(0,0,2),M(0,,1),N(1,0,2).(1)证明:依题意得DC=(0,2,0),DE=(2,0,2).设n0=(x,y,z)为平面CDE的法向量,则即不妨令z=-1,可得n0=(1,0,-1).又MN=(1,-,1),可得MN·n0=0,又因为直线MN⊄平面CDE,所以MN∥平面CDE.(2)依题意,可得BC=(-1,0,0),BE=(1,-2,2),CF=(0,-1,2).设n=(x,y,z)为平面BCE的法向量,则即不妨令z=1,可得n=(0,1,1).设m=(x,y,z)为平面BCF的法向量,则即不妨令z=1,可得m=(0,2,1).因此有cos〈m,n〉==,于是sin〈m,n〉=.所以,二面角EBCF的正弦值为.(3)设线段DP的长为h(h∈[0,2]),则点P的坐标为(0,0,h),可得BP=(-1,-2,h).易知,DC=(0,2,0)为平面ADGE的一个法向量,故|cos〈BP,DC〉|==,由题意,可得=sin60°=,解得h=∈[0,2].所以,线段DP的长为.4.如图,底面为正方形的四棱锥EABCD中,BE⊥平面ABCD,点F,G分别在棱AB,EC上,且满足AF=2FB,CE=3CG.(1)求证:FG∥平面ADE;(2)若BE=AB,求二面角FEGB的正弦值.解析:(1)证明:在棱BE上取点H,使得EH=2HB,连接FH,GH(图略),因为AF=2FB,EH=2HB,所以FH∥AE.同理可证GH∥BC.3又FH⊄平面ADE,AE⊂平面ADE,所以FH∥平面ADE.因为BC∥AD,所以GH∥AD.又GH⊄平面ADE,AD⊂平面ADE,所以GH∥平面ADE.因为FH∩GH=H,所以平面FGH∥平面ADE.因为FG⊂平面FGH,所以FG∥平面ADE.(2)依题意,以B为坐标原点,BA,BE,BC的方向分别为x,y,z轴的正方向,建立如图所示的空间直角坐标系B-xyz,设AB=3,则F(1,0,0),E(0,3,0),G(0,1,2),所以FE=(-1,3,0),FG=(-1,1,2).设平面EFG的法向量为n=(x,y,z),则即取x=3,则n=(3,1,1)为平面EFG的一个法向量.又平面EGB的法向量,即平面ECB的法向量,则BA=(3,0,0)为平面EGB的一个法向量,所以cos〈n,BA〉===,又二面角FEGB为锐角,所以二面角FEGB的余弦值为,所以二面角FEGB的正弦值为=.4