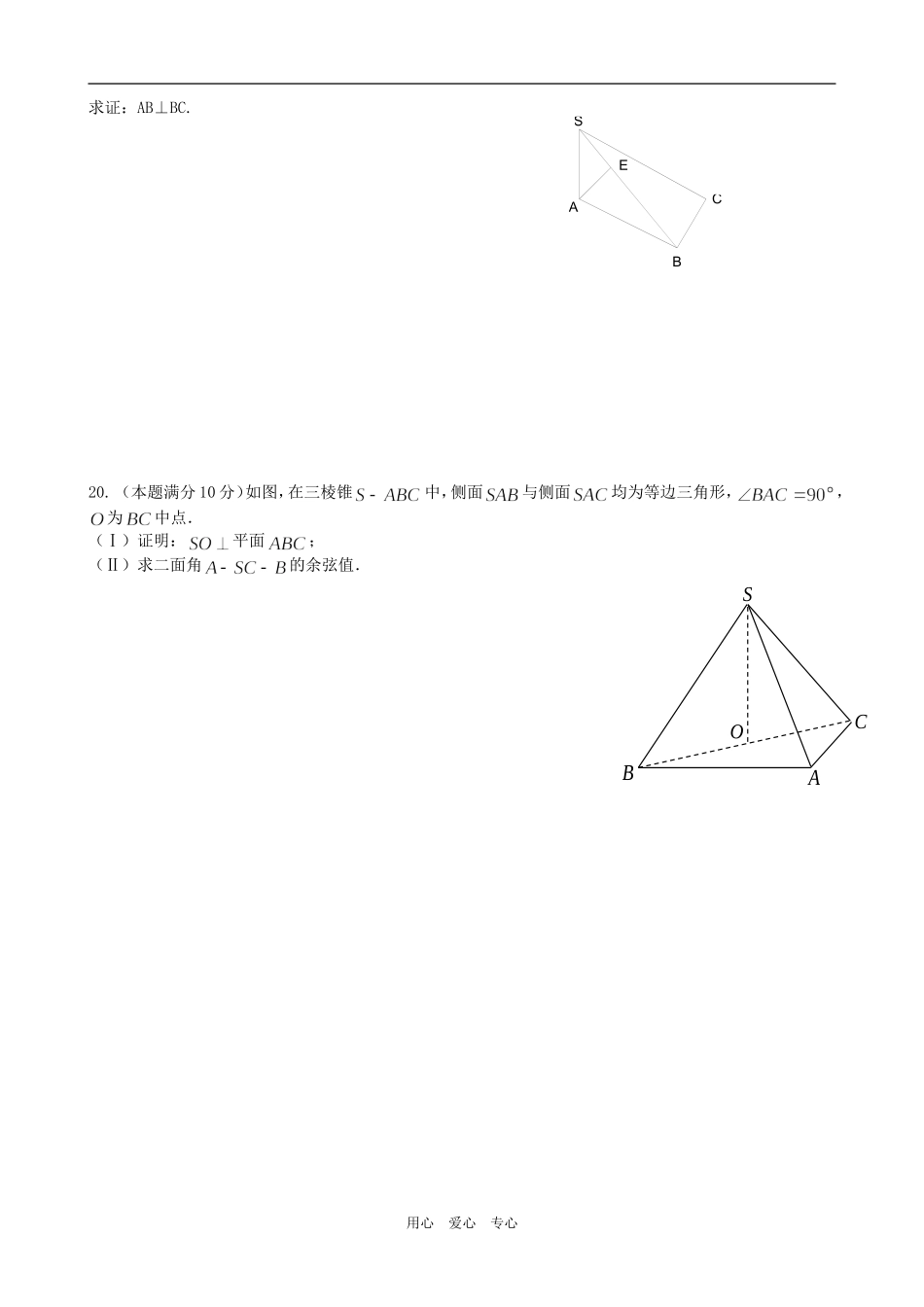
立体几何检测题(时间:90分钟,满分:100分)班别学号姓名成绩一、填空题(3×12=36)1、已知是两条异面直线,,那么与的位置关系____________________.2、已知直线a//平面,平面//平面,则直线a与平面的位置关系为.3、如图,在侧棱和底面垂直的四棱柱中,当底面满足条件时,有(写出你认为正确的一种条件即可。)4、点到平面的距离分别为和,则线段的中点到平面的距离为_________.5、正方体中,分别是的中点,则与对角面所成角的度数是.6、直二面角--的棱上有一点,在平面内各有一条射线,与成,,则.7、二面角为60º,如果平面内一点到平面的距离为,则在平面上的射影到平面的距离为.8、在边长为的等边三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=,这时二面角B-AD-C的大小为.9、、、是两两垂直且交于点的三个平面,到平面、、的距离分别是2、3、6,则.10、已知在四面体中,分别是的中点,若,则与所成的角的度数为.11、、是两个不同的平面,、是平面及之外的两条不同直线,给出四个论断:①②③④以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:_______________.12、已知、是直线,、是平面,给出下列命题:①若垂直于内的两条相交直线,则l;②若平行于,则平行内所有直线;③若mllm,,,且则;④若ll,且,则;⑤若mlm,,,且∥则∥.其中正确的命题的序号是(注:把你认为正确的命题的序号都填上).用心爱心专心ABCDA1B1C1D1二、选择题(3×4=12)13、如图,将无盖正方体纸盒展开,直线AB,CD在原正方体中的位置关系是()A.平行B.相交且垂直C.异面D.相交成60°14、一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角的关系()A.相等B.互补C.相等或互补D.不能确定15、如图正方形OABC的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的周长是()A.8cmB.6cmC.2(1+)cmD.2(1+)cm16、正四面体中,在棱上,在棱上,使得,记,中表示与所成的角,表示与所成角,则()A.在单调递增B.在单调递减C.在单调递增,而在单调递减D.在为常数三、解答题(10+10+10+10+12=52)。17、(本题满分10分)如图,已知平面⊥平面,,直线(在平面外),求证:。18、(本题满分10分)已知,,,,,∥;求证:是异面直线.19.(本题满分10分)如图,S为△ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC。用心爱心专心xyCBAODCABbc求证:AB⊥BC.20.(本题满分10分)如图,在三棱锥中,侧面与侧面均为等边三角形,,为中点.(Ⅰ)证明:平面;(Ⅱ)求二面角的余弦值.用心爱心专心EABCSOSBAC21.(本题满分12分)如图,为空间四点.在中,.等边三角形以为轴运动.(Ⅰ)当平面平面时,求;(Ⅱ)当转动时,是否总有?证明你的结论.用心爱心专心DBAC